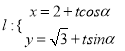题目内容
【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足![]()
![]() , ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
, ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A.(![]() ,
,![]() )
)
B.(![]() ,3)
,3)
C.(![]() , 1)
, 1)
D.(![]() , 1)
, 1)
【答案】C
【解析】解:由题意可知,∵f(x)=x3﹣x2+a,f′(x)=3x2﹣2x
在区间[0,a]存在x1 , x2(a<x1<x2<b),
满足f′(x1)=f′(x2)=![]() =a2﹣a,
=a2﹣a,
∵f(x)=x3﹣x2+a,
∴f′(x)=3x2﹣2x,
∴方程3x2﹣2x=a2﹣a在区间(0,a)有两个不相等的解.
令g(x)=3x2﹣2x﹣a2+a,(0<x<a)
则 ,
,
解得;![]() .
.
∴实数a的取值范围是(![]() , 1)
, 1)
故选:C
【考点精析】认真审题,首先需要了解导数的几何意义(通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ).
).

【题目】某服装销售公司进行关于消费档次的调查,根据每人月均服装消费额将消费档次分为0-500元;500-1000元;1000-1500元;1500-2000元四个档次,针对![]() 两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
| 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
A类 | 20 | 50 | 20 | 10 |
B类 | 50 | 30 | 10 | 10 |
月均服装消费额不超过1000元的人群视为中低消费人群,超过1000元的视为中高收入人群.
(Ⅰ)从![]() 类样本中任选一人,求此人属于中低消费人群的概率;
类样本中任选一人,求此人属于中低消费人群的概率;
(Ⅱ)从![]() 两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(Ⅲ)以各消费档次的区间中点对应的数值为该档次的人均消费额,估计![]() 两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).