题目内容
袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是| 1 |
| 3 |
(Ⅰ)从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
(i)求恰好摸5次停止的概率;
(ii)记5次之内(含5次)摸到红球的次数为ξ,求随机变量ξ的分布率及数学期望Eξ.
(Ⅱ)若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是
| 2 |
| 5 |
分析:(I)(i)由题意知本题是在相同的条件下进行的试验,且事件发生的概率相同,可以看作独立重复试验,恰好摸5次停止表示第次一定摸到红球,前四次有两次摸到红球,根据独立重复试验公式得到结果.
(ii)由题意知从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止,随机变量ξ的取值为0,1,2,3;由n次独立重复试验概率公式得到概率,写出分布列和期望.
(2)由题意知本题是一个古典概型,试验发生的所有事件是3m,而满足条件的是
m+2mp,根据古典概型公式得到关于P的方程,解方程即可.
(ii)由题意知从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止,随机变量ξ的取值为0,1,2,3;由n次独立重复试验概率公式得到概率,写出分布列和期望.
(2)由题意知本题是一个古典概型,试验发生的所有事件是3m,而满足条件的是
| 1 |
| 3 |
解答: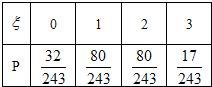 解:(Ⅰ)(i)由题意知本题是在相同的条件下进行的试验,且事件发生的概率相同,可以看作独立重复试验,恰好摸5次停止表示第五次一定摸到红球,前四次有两次摸到红球,根据独立重复试验公式得到
解:(Ⅰ)(i)由题意知本题是在相同的条件下进行的试验,且事件发生的概率相同,可以看作独立重复试验,恰好摸5次停止表示第五次一定摸到红球,前四次有两次摸到红球,根据独立重复试验公式得到
C42×(
)2×(
)2×
=
.
(ii)由题意知从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止
∴随机变量ξ的取值为0,1,2,3;
由n次独立重复试验概率公式Pn(k)=Cnkpk(1-p)n-k,得
P(ξ=0)=C50×(1-
)5=
;
P(ξ=1)=C51×
×(1-
)4=
;
P(ξ=2)=C52×(
)2×(1-
)3=
;
P(ξ=3)=
(
)3+
•(
)2•
•
+
(
)2(
)2•
=
.
随机变量ξ的分布列是
∴ξ的数学期望是Eξ=
×0+
×1+
×2+
×3=
.
(Ⅱ)由题意知本题是一个古典概型,
设袋子A中有m个球,则袋子B中有2m个球.
试验发生的所有事件是3m,
而满足条件的是
m+2mp,
根据古典概型公式得到
=
,
∴p=
.
 解:(Ⅰ)(i)由题意知本题是在相同的条件下进行的试验,且事件发生的概率相同,可以看作独立重复试验,恰好摸5次停止表示第五次一定摸到红球,前四次有两次摸到红球,根据独立重复试验公式得到
解:(Ⅰ)(i)由题意知本题是在相同的条件下进行的试验,且事件发生的概率相同,可以看作独立重复试验,恰好摸5次停止表示第五次一定摸到红球,前四次有两次摸到红球,根据独立重复试验公式得到C42×(
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 81 |
(ii)由题意知从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止
∴随机变量ξ的取值为0,1,2,3;
由n次独立重复试验概率公式Pn(k)=Cnkpk(1-p)n-k,得
P(ξ=0)=C50×(1-
| 1 |
| 3 |
| 32 |
| 243 |
P(ξ=1)=C51×
| 1 |
| 3 |
| 1 |
| 3 |
| 80 |
| 243 |
P(ξ=2)=C52×(
| 1 |
| 3 |
| 1 |
| 3 |
| 80 |
| 243 |
P(ξ=3)=
| C | 3 3 |
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 17 |
| 81 |
随机变量ξ的分布列是
∴ξ的数学期望是Eξ=
| 32 |
| 243 |
| 80 |
| 243 |
| 80 |
| 243 |
| 51 |
| 243 |
| 131 |
| 81 |
(Ⅱ)由题意知本题是一个古典概型,
设袋子A中有m个球,则袋子B中有2m个球.
试验发生的所有事件是3m,
而满足条件的是
| 1 |
| 3 |
根据古典概型公式得到
| ||
| 3m |
| 2 |
| 5 |
∴p=
| 13 |
| 30 |
点评:解决离散型随机变量分布列问题时,主要依据概率的有关概念和运算,同时还要注意题目中离散型随机变量服从什么分布,若服从特殊的分布则运算要简单的多.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目