题目内容
已知f(x)=2ax-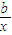 +lnx在x=-1,x=
+lnx在x=-1,x= 处取得极值.
处取得极值.(1)求a、b的值;
(2)若对x∈[
 ,4]时,f(x)>c恒成立,求c的取值范围.
,4]时,f(x)>c恒成立,求c的取值范围.
【答案】分析:(1)先对函数f(x)进行求导,根据f'(-1)=0,f'( )=0求出a,b的值.
)=0求出a,b的值.
(2)先将问题转化为求函数f(x)在[ ,4]最小值的问题,只要c小于f(x)在[
,4]最小值的问题,只要c小于f(x)在[ ,4]最小值即可满足条件.
,4]最小值即可满足条件.
将a,b的值代入f'(x),然后判断函数的单调性,进而可求最小值.
解答:解:(1)∵f(x)=2ax- +lnx,
+lnx,
∴f′(x)=2a+ +
+ .
.
∵f(x)在x=-1与x= 处取得极值,
处取得极值,
∴f′(-1)=0,f′( )=0,
)=0,
即 解得
解得
∴所求a、b的值分别为1、-1.
(2)由(1)得f′(x)=2- +
+ =
= (2x2+x-1)=
(2x2+x-1)= (2x-1)(x+1).
(2x-1)(x+1).
∴当x∈[ ,
, ]时,f′(x)<0;
]时,f′(x)<0;
当x∈[ ,4]时,f′(x)>0.
,4]时,f′(x)>0.
∴f( )是f(x)在[
)是f(x)在[ ,4]上的极小值.又∵只有一个极小值,
,4]上的极小值.又∵只有一个极小值,
∴f(x)min=f( )=3-ln2.
)=3-ln2.
∵f(x)>c恒成立,∴c<f(x)min=3-ln2.
∴c的取值范围为c<3-ln2.
点评:本题主要考查函数的单调性、极值点与其导函数的关系.导数是高考的热点问题,每年必考,要重视.
 )=0求出a,b的值.
)=0求出a,b的值.(2)先将问题转化为求函数f(x)在[
 ,4]最小值的问题,只要c小于f(x)在[
,4]最小值的问题,只要c小于f(x)在[ ,4]最小值即可满足条件.
,4]最小值即可满足条件.将a,b的值代入f'(x),然后判断函数的单调性,进而可求最小值.
解答:解:(1)∵f(x)=2ax-
 +lnx,
+lnx,∴f′(x)=2a+
 +
+ .
.∵f(x)在x=-1与x=
 处取得极值,
处取得极值,∴f′(-1)=0,f′(
 )=0,
)=0,即
 解得
解得
∴所求a、b的值分别为1、-1.
(2)由(1)得f′(x)=2-
 +
+ =
= (2x2+x-1)=
(2x2+x-1)= (2x-1)(x+1).
(2x-1)(x+1).∴当x∈[
 ,
, ]时,f′(x)<0;
]时,f′(x)<0;当x∈[
 ,4]时,f′(x)>0.
,4]时,f′(x)>0.∴f(
 )是f(x)在[
)是f(x)在[ ,4]上的极小值.又∵只有一个极小值,
,4]上的极小值.又∵只有一个极小值,∴f(x)min=f(
 )=3-ln2.
)=3-ln2.∵f(x)>c恒成立,∴c<f(x)min=3-ln2.
∴c的取值范围为c<3-ln2.
点评:本题主要考查函数的单调性、极值点与其导函数的关系.导数是高考的热点问题,每年必考,要重视.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
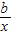 +lnx在x=-1,x=
+lnx在x=-1,x= 处取得极值.
处取得极值. ,4]时,f(x)>c恒成立,求c的取值范围.
,4]时,f(x)>c恒成立,求c的取值范围.