题目内容
已知f(x)=2ax-
+4lnx在x=1与x=
都取得极值.
(1)求a、b;
(2)若对x∈[
,e]时,f(x)≥c取值范围.
| b |
| x |
| 1 |
| 3 |
(1)求a、b;
(2)若对x∈[
| 1 |
| e |
分析:(1)求导数f′(x),由f(x)在x=1与x=
处取得极值得f′′(1)=0,f′′(
)=0,从而得到方程组,解出a,b再加以检验;
(2)利用导数求出f(x)的单调区间,结合图象通过作差比较出f(x)在[
,e]上的最小值,则f(x)≥c恒成立等价于f(x)min≥c;
| 1 |
| 3 |
| 1 |
| 3 |
(2)利用导数求出f(x)的单调区间,结合图象通过作差比较出f(x)在[
| 1 |
| e |
解答:解:(1)f′(x)=2a+
+
,
∵f(x)=2ax-
+4lnx在x=1与x=
处都取得极值,
∴f′(1)=0,f′(
)=0,
∴
,解得a=-
,b=-1,
经检验符合题意;
(2)由(1)可知f(x)=-3x+
+4lnx,
f′′(x)=-3-
+
=-
,
由f′(x)≥0,得f(x)的单调增区间为[
,1],
由f′(x)≤0,得f(x)的单调减区间为(0,
]和[1,+∞),
当x∈[
,e]时,f(
)=e-4-
,f(e)=
+4-3e,
而f(
)-f(e)=4e-8-
>0,
所以f(
)>f(e),即f(x)在[
,e]上的最小值为
+4-3e,
要使对x∈[
,e]时,f(x)≥c恒成立,必须c≤f(x)min=
+4-3e.
| b |
| x2 |
| 4 |
| x |
∵f(x)=2ax-
| b |
| x |
| 1 |
| 3 |
∴f′(1)=0,f′(
| 1 |
| 3 |
∴
|
| 3 |
| 2 |
经检验符合题意;
(2)由(1)可知f(x)=-3x+
| 1 |
| x |
f′′(x)=-3-
| 1 |
| x2 |
| 4 |
| x |
| (3x-1)(x-1) |
| x2 |
由f′(x)≥0,得f(x)的单调增区间为[
| 1 |
| 3 |
由f′(x)≤0,得f(x)的单调减区间为(0,
| 1 |
| 3 |
当x∈[
| 1 |
| e |
| 1 |
| e |
| 3 |
| e |
| 1 |
| e |
而f(
| 1 |
| e |
| 4 |
| e |
所以f(
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
要使对x∈[
| 1 |
| e |
| 1 |
| e |
点评:本题考查利用导数求函数在闭区间上的最值、函数在某点取得极值的条件,考查恒成立问题的处理,转化为求函数最值是解决恒成立问题的常用方法.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
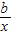 +lnx在x=-1,x=
+lnx在x=-1,x= 处取得极值.
处取得极值. ,4]时,f(x)>c恒成立,求c的取值范围.
,4]时,f(x)>c恒成立,求c的取值范围.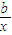 +lnx在x=-1,x=
+lnx在x=-1,x= 处取得极值.
处取得极值. ,4]时,f(x)>c恒成立,求c的取值范围.
,4]时,f(x)>c恒成立,求c的取值范围.