Question

【题目】如图，已知圆：，点是圆内一个定点，点是圆上任意一点，线段的垂直平分线和半径相交于点.当点在圆上运动时，点的轨迹为曲线.

（1）求曲线的方程；

（2）设过点的直线与曲线相交于两点（点在两点之间）.是否存在直线使得？若存在，求直线的方程；若不存在，请说明理由.

Answer 1

【答案】（1）（2）存在，或．

【解析】

（1）结合垂直平分线的性质和椭圆的定义，求出椭圆的方程.

（2）设出直线的方程，联立直线的方程和椭圆方程，写出韦达定理，利用，结合向量相等的坐标表示，求得直线的斜率，进而求得直线的方程.方法一和方法二的主要曲边是直线的方程的设法的不同.

（1）因为圆的方程为，

所以，半径．

因为是线段的垂直平分线，所以．

所以．

因为，

所以点的轨迹是以，为焦点，长轴长的椭圆．

因为，，，

所以曲线的方程为．

（2）存在直线使得．

方法一：因为点在曲线外，直线与曲线相交，

所以直线的斜率存在，设直线的方程为．

设，

由 得．

则， ①

， ②

由题意知，解得．

因为，

所以，即． ③

把③代入①得， ④

把④代入②得，得，满足．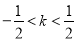

所以直线的方程为：或．

方法二：因为当直线的斜率为0时，，，，

此时．

因此设直线的方程为：．

设，

由 得．

由题意知，解得或，

则， ①

， ②

因为，所以． ③

把③代入①得， ④

把④代入②得，，满足或．

所以直线的方程为或．