题目内容
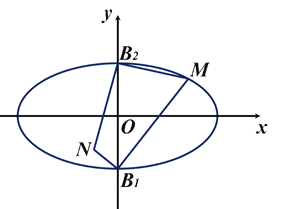
【题目】已知椭圆
：
的短轴端点为
，
，点
是椭圆上的动点，且不与，重合，点
满足
，
.
（Ⅰ）求动点的轨迹方程；
（Ⅱ）求四边形
面积的最大值.
【答案】（Ⅰ）
；（Ⅱ）
.
【解析】
（Ⅰ）设
，
，结合垂直关系设出两直线的方程，相乘即可得到动点
的轨迹方程；
（Ⅱ）利用根与系数的关系表示四边形
面积，转求函数最值即可.
（Ⅰ）法一：设，，
直线
直线
得
又
，
，
整理得点的轨迹方程为
法二：设，，
直线
直线
由,解得：
，又
，
故
，代入得
.
点的轨迹方程为
法三：设直线
，则直线
直线
与椭圆
的交点
的坐标为
.
则直线
的斜率为
.
直线
由 解得:点的轨迹方程为：
（Ⅱ）法一：设
，由（Ⅰ）法二得：
四边形的面积
，
，当
时，
的最大值为.
法二：由（Ⅰ）法三得：四边形的面积
当且仅当
时，取得最大值.
练习册系列答案
相关题目
【题目】在对人们的休闲方式的一次调查中，共调查了110人，其中女性50人，男性60人.女性中有30人主要的休闲方式是看电视，另外20人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外40人主要的休闲方式是运动.
（1）根据以上数据建立一个
列联表；
（2）判断是否有99%的把握认为性别与休闲方式有关系.
下面临界值表供参考：
| 0.10 | 0.05 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
（参考公式：
）
