题目内容
设a>2,x∈R,M=a+A.M<N B.M>N C.M≤N D.M≥N
D
解析:∵a>2,∴a-2>0.∴M=a+![]() =(a-2)+
=(a-2)+![]() +2≥4.
+2≥4.
又N=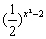 ≤(
≤(![]() )-2=4,∴M≥N.
)-2=4,∴M≥N.
故应选D.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
题目内容
设a>2,x∈R,M=a+A.M<N B.M>N C.M≤N D.M≥N
D
解析:∵a>2,∴a-2>0.∴M=a+![]() =(a-2)+
=(a-2)+![]() +2≥4.
+2≥4.
又N=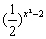 ≤(
≤(![]() )-2=4,∴M≥N.
)-2=4,∴M≥N.
故应选D.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案