题目内容
已知函数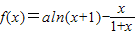 在[0,+∞)上单调递增,数列{an}满足
在[0,+∞)上单调递增,数列{an}满足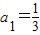 ,
,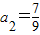 ,
,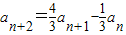 (n∈N*).
(n∈N*).(Ⅰ)求实数a的取值范围以及a取得最小值时f(x)的最小值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)求证:
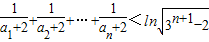 (n∈N*).
(n∈N*).
【答案】分析:(Ⅰ)由题意,f′(x)= ≥0在[0,+∞)上恒成立,分离参数,可得a≥
≥0在[0,+∞)上恒成立,分离参数,可得a≥ 在[0,+∞)上恒成立,求出最值,即可得到结论;
在[0,+∞)上恒成立,求出最值,即可得到结论;
(Ⅱ)先证明{ }是常数数列,再证明{an-1}是首项为-
}是常数数列,再证明{an-1}是首项为- ,公比为
,公比为 的等比数列,即可求数列{an}的通项公式;
的等比数列,即可求数列{an}的通项公式;
(Ⅲ)由(Ⅰ)知 对x∈[0,+∞)恒成立,令x=
对x∈[0,+∞)恒成立,令x= ,则
,则 ,可得
,可得 <ln(3n+1-2)-ln(3n-2),叠加即可证得结论.
<ln(3n+1-2)-ln(3n-2),叠加即可证得结论.
解答:(Ⅰ)解:由题意,f′(x)= ≥0在[0,+∞)上恒成立
≥0在[0,+∞)上恒成立
∴a≥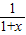 在[0,+∞)上恒成立
在[0,+∞)上恒成立
∵x∈[0,+∞),∴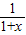 ∈(0,1]
∈(0,1]
∴a≥1
当a=1时,f(x)min=f(0)=0;
(Ⅱ)解:∵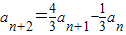 ,
,
∴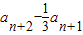 =
=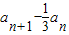
∴{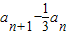 }是常数数列
}是常数数列
∵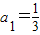 ,
,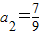 ,
,
∴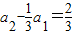
∴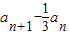 =
=
∴
∴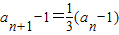
∴{an-1}是首项为- ,公比为
,公比为 的等比数列
的等比数列
∴an-1=(- )•
)•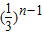
∴an=1-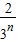 ;
;
(Ⅲ)证明:由(Ⅰ)知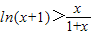 对x∈[0,+∞)恒成立
对x∈[0,+∞)恒成立
令x=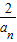 ,则
,则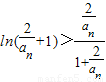
∴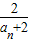 <ln(
<ln( +1)=ln(3n+1-2)-ln(3n-2)
+1)=ln(3n+1-2)-ln(3n-2)
∴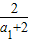 +
+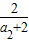 +…+
+…+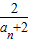 <[ln(32-2)-ln(31-2)]+[ln(33-2)-ln(32-2)]+…+ln(3n+1-2)-ln(3n-2)=ln(3n+1-2)
<[ln(32-2)-ln(31-2)]+[ln(33-2)-ln(32-2)]+…+ln(3n+1-2)-ln(3n-2)=ln(3n+1-2)
∴
点评:本题考查导数知识的运用,考查数列的通项与不等式的证明,考查学生分析解决问题的能力,属于中档题.
 ≥0在[0,+∞)上恒成立,分离参数,可得a≥
≥0在[0,+∞)上恒成立,分离参数,可得a≥ 在[0,+∞)上恒成立,求出最值,即可得到结论;
在[0,+∞)上恒成立,求出最值,即可得到结论;(Ⅱ)先证明{
 }是常数数列,再证明{an-1}是首项为-
}是常数数列,再证明{an-1}是首项为- ,公比为
,公比为 的等比数列,即可求数列{an}的通项公式;
的等比数列,即可求数列{an}的通项公式;(Ⅲ)由(Ⅰ)知
 对x∈[0,+∞)恒成立,令x=
对x∈[0,+∞)恒成立,令x= ,则
,则 ,可得
,可得 <ln(3n+1-2)-ln(3n-2),叠加即可证得结论.
<ln(3n+1-2)-ln(3n-2),叠加即可证得结论.解答:(Ⅰ)解:由题意,f′(x)=
 ≥0在[0,+∞)上恒成立
≥0在[0,+∞)上恒成立∴a≥
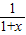 在[0,+∞)上恒成立
在[0,+∞)上恒成立∵x∈[0,+∞),∴
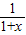 ∈(0,1]
∈(0,1]∴a≥1
当a=1时,f(x)min=f(0)=0;
(Ⅱ)解:∵
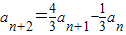 ,
,∴
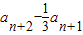 =
=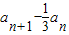
∴{
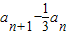 }是常数数列
}是常数数列∵
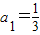 ,
,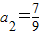 ,
,∴
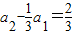
∴
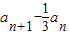 =
=
∴

∴
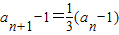
∴{an-1}是首项为-
 ,公比为
,公比为 的等比数列
的等比数列∴an-1=(-
 )•
)•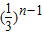
∴an=1-
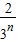 ;
;(Ⅲ)证明:由(Ⅰ)知
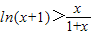 对x∈[0,+∞)恒成立
对x∈[0,+∞)恒成立令x=
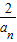 ,则
,则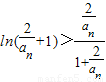
∴
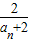 <ln(
<ln( +1)=ln(3n+1-2)-ln(3n-2)
+1)=ln(3n+1-2)-ln(3n-2)∴
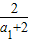 +
+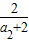 +…+
+…+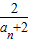 <[ln(32-2)-ln(31-2)]+[ln(33-2)-ln(32-2)]+…+ln(3n+1-2)-ln(3n-2)=ln(3n+1-2)
<[ln(32-2)-ln(31-2)]+[ln(33-2)-ln(32-2)]+…+ln(3n+1-2)-ln(3n-2)=ln(3n+1-2)∴

点评:本题考查导数知识的运用,考查数列的通项与不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 在[0,+
在[0,+ )上最小值是
)上最小值是
 的通项公式;
的通项公式; ,求证:
,求证: ;
; 在[0,+
在[0,+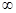 )上最小值是
)上最小值是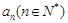
 的通项公式;
的通项公式; ,求证:
,求证: ;
;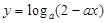 在[0,1]上是
在[0,1]上是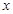 的减函数,则
的减函数,则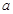 的取值范围是(
)
的取值范围是(
)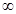 )
)
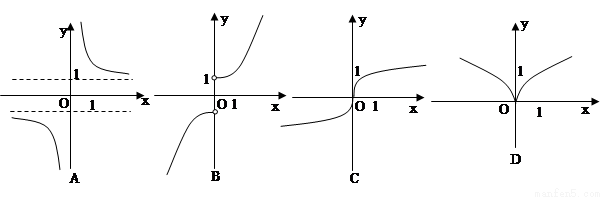
 在[0,1]上是减函数,则a的取值范围是( )
在[0,1]上是减函数,则a的取值范围是( ) B.(1,2) C.
B.(1,2) C. D.
D.
