题目内容
7.已知椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{8}$=1的右焦点F(1,0),定点A(2,1),P为椭圆上一动点,则PA+3PF的最小值为7.分析 通过椭圆右焦点F(1,0)可知椭圆方程为:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1,进而可知离心率e=$\frac{1}{3}$、准线方程为x=±9,利用椭圆第二定义可知PA+3PF的最小值即为点A到右准线的距离AB,计算即得结论.
解答 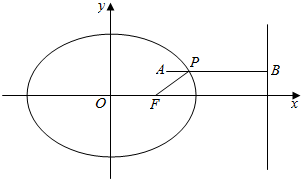 解:∵椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{8}$=1的右焦点F(1,0),
解:∵椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{8}$=1的右焦点F(1,0),
∴m=8+1=9,即椭圆方程为:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1,
∴离心率e=$\frac{c}{a}$=$\frac{1}{3}$,准线方程为:x=±$\frac{{a}^{2}}{c}$=±9,
由椭圆第二定义可知3PF即为点P到右准线的距离,
从而PA+3PF的最小值即为点A到右准线的距离AB,
又∵A(2,1),
∴AB=xB-xA=9-2=7,
故答案为:7.
点评 本题考查椭圆的第二定义,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
