��Ŀ����
��֪����{bn}��������������T����һ��n��N*����bn+r=bn���������{bn}Ϊ�������У�T������һ�����ڣ����磺����a��a��a��a�����ٿɿ�������Ϊ1�����У�
����a��b��a��b�����ڿɿ�������Ϊ2�����У�
����a��b��c��a��b��c�����ۿɿ�������Ϊ3�����С�
��1���������Тڣ�����һ��ͨ�ʽ������
 ������д�������е�һ��ͨ�ʽ��
������д�������е�һ��ͨ�ʽ����2�������Т۵�ǰn���Sn��
��3������������a=2��b=
 ��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|��
��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|�� ��������е�һ��ͨ�ʽbn��
��������е�һ��ͨ�ʽbn��
���𰸡���������1����������a��b��a��b�����ɿ�������Ϊ2�����У���д�����е�ͨ�
��2������a��b��c��a��b��c�����ɿ�������Ϊ3�����У��ʿɷ���ó����ۣ�
��3�������⣬�أ�0��Ӧ�� ���æ�=
���æ�= ������bn=Asin��
������bn=Asin�� n+�գ�+B����b1=2��b2=
n+�գ�+B����b1=2��b2= ��b3=-1��������ʽ�����ɵó����ۣ�
��b3=-1��������ʽ�����ɵó����ۣ�
����⣺��1��������a��b��a��b�����ɿ�������Ϊ2�����У�
��an= �ȣ���3�֣�
�ȣ���3�֣�
��2������a��b��c��a��b��c�����ɿ�������Ϊ3�����У����Ե�n=3k+1ʱ�� ����5�֣�
����5�֣�
��n=3k+2ʱ�� ����7�֣�
����7�֣�
��n=3k+3ʱ�� ��k��N������9�֣�
��k��N������9�֣�
��3�������⣬�أ�0��Ӧ�� ���æ�=
���æ�= ����10�֣�
����10�֣�
����bn=Asin�� n+�գ�+B��
n+�գ�+B��
��b1=2��b2= ��b3=-1��������ʽ��
��b3=-1��������ʽ�� ��12�֣�
��12�֣�
�ɣ�1����2���ɵ�Acos��= ���ٴ��루1����չ��ʽ���ɵ�-
���ٴ��루1����չ��ʽ���ɵ�- ��+B=
��+B= ���루3��������B=
���루3��������B= ����13�֣�
����13�֣�
Asin��=- ������tan��=-
������tan��=-
��Ϊ|��|�� �����Ԧ�=-
�����Ԧ�=- ����14�֣�
����14�֣�
���ǿ����A= ����15�֣�
����15�֣�
��bn= sin��
sin�� ��+
��+ ��16�֣�
��16�֣�
���������⿼�����������Ǻ������ۺϣ�����ѧ������������������������������۵���ѧ˼�룬��һ���Ѷȣ�
��2������a��b��c��a��b��c�����ɿ�������Ϊ3�����У��ʿɷ���ó����ۣ�
��3�������⣬�أ�0��Ӧ��
 ���æ�=
���æ�= ������bn=Asin��
������bn=Asin�� n+�գ�+B����b1=2��b2=
n+�գ�+B����b1=2��b2= ��b3=-1��������ʽ�����ɵó����ۣ�
��b3=-1��������ʽ�����ɵó����ۣ�����⣺��1��������a��b��a��b�����ɿ�������Ϊ2�����У�
��an=
 �ȣ���3�֣�
�ȣ���3�֣���2������a��b��c��a��b��c�����ɿ�������Ϊ3�����У����Ե�n=3k+1ʱ��
 ����5�֣�
����5�֣���n=3k+2ʱ��
 ����7�֣�
����7�֣���n=3k+3ʱ��
 ��k��N������9�֣�
��k��N������9�֣���3�������⣬�أ�0��Ӧ��
 ���æ�=
���æ�= ����10�֣�
����10�֣�����bn=Asin��
 n+�գ�+B��
n+�գ�+B����b1=2��b2=
 ��b3=-1��������ʽ��
��b3=-1��������ʽ�� ��12�֣�
��12�֣��ɣ�1����2���ɵ�Acos��=
 ���ٴ��루1����չ��ʽ���ɵ�-
���ٴ��루1����չ��ʽ���ɵ�- ��+B=
��+B= ���루3��������B=
���루3��������B= ����13�֣�
����13�֣�Asin��=-
 ������tan��=-
������tan��=-
��Ϊ|��|��
 �����Ԧ�=-
�����Ԧ�=- ����14�֣�
����14�֣����ǿ����A=
 ����15�֣�
����15�֣���bn=
 sin��
sin�� ��+
��+ ��16�֣�
��16�֣����������⿼�����������Ǻ������ۺϣ�����ѧ������������������������������۵���ѧ˼�룬��һ���Ѷȣ�

��ϰ��ϵ�д�
�����Ŀ
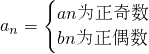 ������д�������е�һ��ͨ�ʽ��
������д�������е�һ��ͨ�ʽ�� ��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|��
��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|�� ��������е�һ��ͨ�ʽbn��
��������е�һ��ͨ�ʽbn��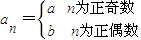 ������д�������е�һ��ͨ�ʽ��
������д�������е�һ��ͨ�ʽ�� ��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|��
��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|��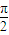 ��������е�һ��ͨ�ʽbn��
��������е�һ��ͨ�ʽbn��