Question

设有半径为3 km的圆形村落，A、B两人同时从村落中心出发，B向北直行，A先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线前进，后来恰与B相遇.设A、B两人速度一定，其速度比为3∶1，问两人在何处相遇？

Answer 1

思路分析：因为A、B两人速度一定，其速度比为3∶1，可以先把其速度设出来.在这个问题中的关键是：路程之间的关系满足勾股定理，根据它可以建立一个关系式.

解：如图1-1-4建立平面直角坐标系，由题意可设A、B两人速度分别为3v千米/时，v千米/时，再设出发x₀小时，在点P改变方向，又经过y₀小时，在点Q处与B相遇,

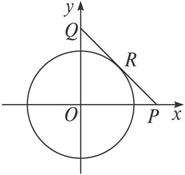
图1-1-4

则P、Q两点坐标为(3vx₀,0)，(0,vx₀+vy₀).由|OP|²+|OQ|²=|PQ|²,知(3vx₀)²+(vx₀+vy₀)²=(3vy₀)²，即(x₀+y₀)(5x₀-4y₀)=0.

∵x₀+y₀＞0,∴5x₀=4y₀①.将①代入k_PQ=，得k_PQ=.

又已知PQ与圆O相切，直线PQ在y轴上的截距就是两人相遇的位置.

设直线y=x+b与圆O:x²+y²=9相切，则有=3.∴b=.

答：A、B两人的相遇点在离村中心正北千米处.

    方法归纳 在实际问题中能够根据已知条件合理地建立坐标系是个很关键的问题.本题当中,注意到村落为圆形，且A、B两人同时从村落中心出发分别沿东、北方向运动，于是可设想以村落的中心为圆点，以开始时A、B的前进方向为x、y轴，建立直角坐标系.