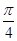题目内容
(本小题满分14分)
给定椭圆 :
: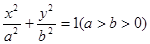 . 称圆心在原点
. 称圆心在原点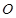 ,半径为
,半径为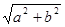 的圆是椭圆
的圆是椭圆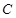 的“准圆”. 若椭圆
的“准圆”. 若椭圆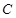 的一个焦点为
的一个焦点为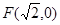 ,其短轴上的一个端点到
,其短轴上的一个端点到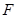 的距离为
的距离为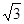 .
.
(1)求椭圆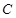 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点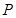 是椭圆
是椭圆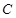 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点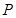 作直线
作直线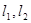 ,使得
,使得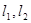 与椭圆
与椭圆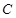 都只有一个交点,试判断
都只有一个交点,试判断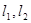 是否垂直?并说明理由.
是否垂直?并说明理由.
给定椭圆
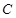 :
: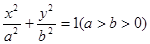 . 称圆心在原点
. 称圆心在原点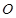 ,半径为
,半径为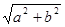 的圆是椭圆
的圆是椭圆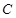 的“准圆”. 若椭圆
的“准圆”. 若椭圆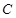 的一个焦点为
的一个焦点为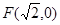 ,其短轴上的一个端点到
,其短轴上的一个端点到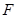 的距离为
的距离为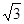 .
.(1)求椭圆
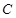 的方程和其“准圆”方程;
的方程和其“准圆”方程;(2)点
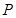 是椭圆
是椭圆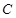 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点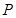 作直线
作直线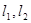 ,使得
,使得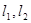 与椭圆
与椭圆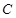 都只有一个交点,试判断
都只有一个交点,试判断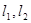 是否垂直?并说明理由.
是否垂直?并说明理由.解:(1)
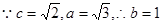 ,
, 椭圆方程为
椭圆方程为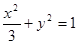 , ………… 4分
, ………… 4分准圆方程为
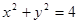 . ……………………5分
. ……………………5分(2)①当
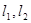 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设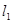 无斜率,
无斜率,因为
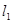 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为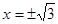 ,
,当
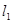 方程为
方程为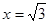 时,此时
时,此时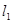 与准圆交于点
与准圆交于点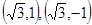 ,
,此时经过点
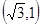 (或
(或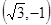 )且与椭圆只有一个公共点的直线是
)且与椭圆只有一个公共点的直线是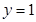 (或
(或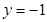 ),即
),即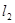 为
为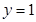 (或
(或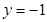 ),显然直线
),显然直线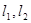 垂直;
垂直;同理可证
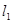 方程为
方程为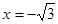 时,直线
时,直线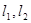 也垂直. ………………8分
也垂直. ………………8分②当
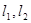 都有斜率时,设点
都有斜率时,设点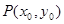 ,其中
,其中 .
.设经过点
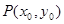 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为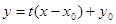 ,
,则由
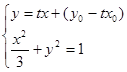 消去
消去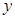 ,得
,得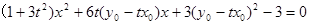 . ………10分
. ………10分由
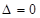 化简整理得:
化简整理得: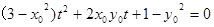 .
. 因为
 ,所以有
,所以有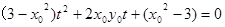 . …11分
. …11分设
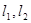 的斜率分别为
的斜率分别为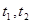 ,因为
,因为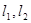 与椭圆只有一个公共点,
与椭圆只有一个公共点,所以
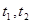 满足上述方程
满足上述方程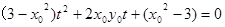 ,
,所以
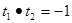 ,即
,即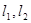 垂直. …………………13分
垂直. …………………13分综合①②知
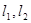 垂直. ……………………14分
垂直. ……………………14分略

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
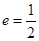 ,过左焦点
,过左焦点 作直线
作直线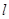 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线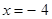 交于点
交于点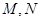 .
.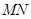 为直径的圆经过焦点
为直径的圆经过焦点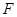 .
. 的左、右焦点,点P在椭圆上,且
的左、右焦点,点P在椭圆上,且 记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1: 2,则该椭圆的离心率等于 ( )
记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1: 2,则该椭圆的离心率等于 ( )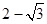
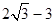

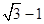
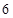 ,短轴长为8,
,短轴长为8,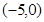 作倾斜角为
作倾斜角为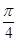 的直线交椭圆C于A、B两点,求
的直线交椭圆C于A、B两点,求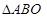 的面积。
的面积。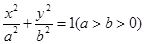 的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,
的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,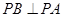 ,则该椭圆的离心率
,则该椭圆的离心率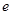 =___▲___.
=___▲___.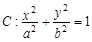 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆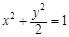 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.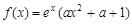
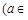 R).
R).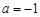 ,求曲线
,求曲线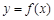 在点
在点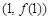 处的的切线方程;
处的的切线方程; 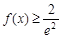 对任意
对任意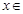
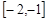 恒成立,求实数
恒成立,求实数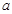 的取值范围.
的取值范围.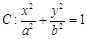
 上的一动点
上的一动点 到右焦点的最短距离为
到右焦点的最短距离为 ,且右焦点到右准线的距离等于短半轴的长.(1)求椭圆
,且右焦点到右准线的距离等于短半轴的长.(1)求椭圆 的方程;
的方程; ,
, 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线 与
与 ;
; 两点,求
两点,求 的取值
的取值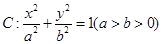 的离心率为
的离心率为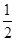 ,直线
,直线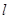 过点
过点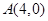 ,
,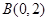 ,且与椭圆
,且与椭圆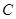 相切于点
相切于点 .
. 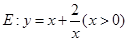 相交于不同的两点
相交于不同的两点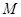 、
、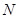 ,曲线
,曲线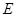 在点
在点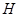 .试问:点
.试问:点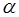 ∈(0,
∈(0,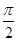 ),方程
),方程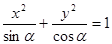 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则