题目内容
3.函数$f(x)=cos(\sqrt{2x-{x^2}})$的单调递增区间是[1,2].分析 设t=2x-x2,则t≥0,解得0≤x≤2,求出t的单调区间,再根据复合函数的单调性即可求出.
解答 解:设t=2x-x2,
则t≥0,解得0≤x≤2,
∴函数t=2x-x2=-(x-1)2+1在[0,1]上为增函数,在(1,2]上为减函数,且0≤t≤1,
∴y=cost在[0,1]上为减函数,
∴$f(x)=cos(\sqrt{2x-{x^2}})$的单调递增区间为[1,2],
故答案为:[1,2].
点评 本题考查了复合函数的单调区间,同增异减,以及三角函数的图象和性质,属于基础题.

练习册系列答案
相关题目
11.记sin35°=a,则tan2015°的值等于( )
| A. | $\frac{a}{{\sqrt{1-{a^2}}}}$ | B. | $\frac{-a}{{\sqrt{1-{a^2}}}}$ | C. | $\frac{{\sqrt{1-{a^2}}}}{a}$ | D. | $\frac{{-\sqrt{1-{a^2}}}}{a}$ |
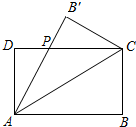 春兰公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能.
春兰公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能.