Question

【题目】已知椭圆：的离心率，点，点、分别为椭圆的上顶点和左焦点，且.

（1）求椭圆的方程；

（2）若过定点的直线与椭圆交于，两点（在，之间）设直线的斜率，在轴上是否存在点，使得以，为邻边的平行四边形为菱形？如果存在，求出的取值范围？如果不存在，请说明理由.

Answer 1

【答案】（1）；（2）存在；.

【解析】

（1）根据离心率，结合的长度，即可列出方程，求解即可；

（2）设出直线方程，联立椭圆方程，由直线和椭圆位置关系，求得的取值范围，结合以及韦达定理，即可容易求得参数范围.

（1）设椭圆焦距为，依题意，有 ①，

由有，有 ②，

又 ③，

由①②③可得，，

椭圆的方程.

（2）设直线的方程为，

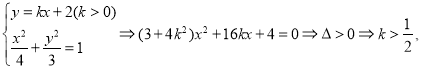
设，

则，

，

，

由于菱形对角线垂直，则，

解得，

即，，

（当且仅当时，等号成立）.

所以存在满足条件的实数，

的取值范围为.