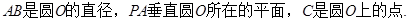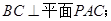题目内容
已知长方体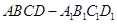 ,点
,点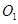 为
为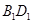 的中点.
的中点.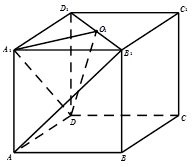
(1)求证: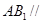 面
面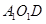 ;
;
(2)若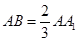 ,试问在线段
,试问在线段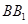 上是否存在点
上是否存在点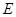 使得
使得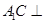
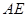 ,若存在求出
,若存在求出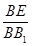 ,若不存在,说明理由.
,若不存在,说明理由.
(1)证明详见解析;(2)存在,证明详见解析.
解析试题分析:(1)设 与
与 的交点为
的交点为 ,由三角形的中位线可证
,由三角形的中位线可证 ∥AB1,,最后根据直线与平面平行的判定定理可证
∥AB1,,最后根据直线与平面平行的判定定理可证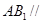 面
面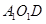 ;(2)假设存在
;(2)假设存在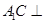
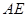 ,连结
,连结 交
交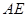 于点
于点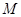 ,由直线与平面垂直的性质定理可得BC⊥AE,由直线与平面垂直的判定定理可得AE⊥平面
,由直线与平面垂直的性质定理可得BC⊥AE,由直线与平面垂直的判定定理可得AE⊥平面 ,即
,即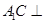
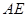 得证.根据两对应角相等,三角形相似证得Rt△ABE~Rt△A1AB,有相似比可证的
得证.根据两对应角相等,三角形相似证得Rt△ABE~Rt△A1AB,有相似比可证的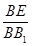 的比值.
的比值.
试题解析:(1)证明:
连结 交
交 于点
于点 ,所以
,所以 为
为 的中点,连结
的中点,连结
 在
在 中,
中,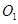 为
为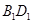 的中点
的中点 4分
4分
 面
面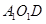 且
且 面
面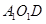
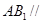 面
面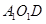 7分
7分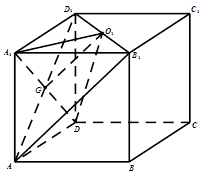
(2)若在线段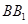 上存在点
上存在点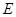 得
得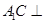
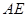 ,连结
,连结 交
交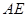 于点
于点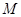
 面
面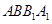 且
且 面
面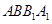

又 且
且 面
面
 面
面
 面
面
 10分
10分
在 和
和 中有:
中有:
 同理:
同理:
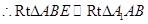 12分
12分

 即在线段
即在线段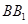 上存在点
上存在点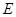 有
有 14分
14分
考点:1.直线与平面平行的判定定理;2.直线与平面垂直的判定和性质定理;3.三角形相似和相似三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

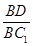 的值.
的值. 所在的平面与正方形
所在的平面与正方形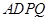 所在的平面相互垂直,
所在的平面相互垂直,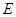 是
是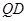 的中点.
的中点.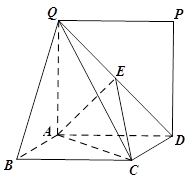
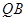 ∥平面
∥平面 ;
;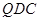 ⊥平面
⊥平面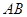 是圆
是圆 的直径,
的直径, 垂直圆
垂直圆 是圆
是圆
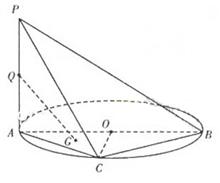
 平面
平面 ;
; 为
为 为
为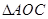 的重心,求证:
的重心,求证: //平面
//平面 .
.
 是正方形,
是正方形, 平面
平面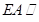
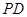 ,
,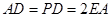 ,
,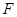 ,
,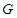 ,
, 分别为
分别为 ,
,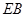 ,
, 的中点.
的中点.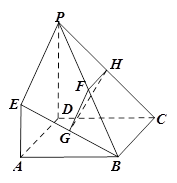
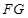
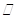 平面
平面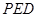 ;
;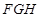 与平面
与平面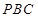 所成锐二面角的大小.
所成锐二面角的大小. 中,
中,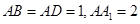 ,点
,点 为
为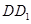 的中点.
的中点.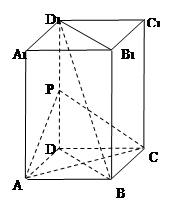
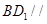 平面
平面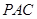 ;
;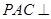 平面
平面 ;
;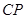 与平面
与平面