题目内容
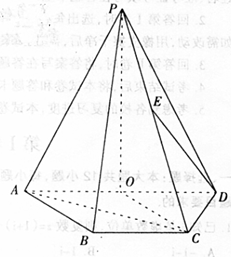
如图,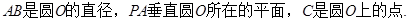
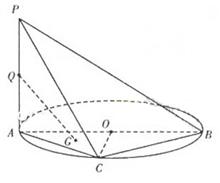
(Ⅰ)求证: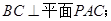
(Ⅱ)设
(Ⅰ) (Ⅱ)均详见解析
解析试题分析:根据线面垂直的判定定理,需在面PAC内证出两条相交线都与BC垂直,首先可根据线面垂直得线线垂直证出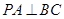 ,再根据圆中直径所对的圆周角为直角,证出
,再根据圆中直径所对的圆周角为直角,证出 , 因为PA与AC相交于点A,所以可以证得
, 因为PA与AC相交于点A,所以可以证得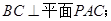 (Ⅱ)因为
(Ⅱ)因为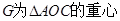 ,延长OG交AC与点M,则M为AC中点,Q为PA中点,所以可得
,延长OG交AC与点M,则M为AC中点,Q为PA中点,所以可得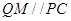 ,根据内线外线平行即可证出
,根据内线外线平行即可证出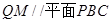 ,同理可证
,同理可证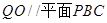 ,因为QM与QO交与点O,所以可得
,因为QM与QO交与点O,所以可得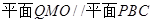 ,因为QG在
,因为QG在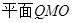 内,所以
内,所以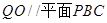
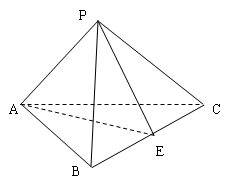
试题解析:(Ⅰ)证明:由AB是圆O的直径,得AC⊥BC.
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC,
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC.
(II)连OG并延长交AC与M,链接QM,QO.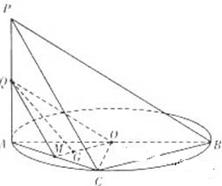
由G为∆AOC的重心,得M为AC中点,
由G为PA中点,得QM//PC.因为,所以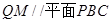
同理可得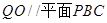 因为
因为 ,
,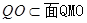 ,
,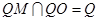 ,所以
,所以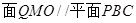 ,因为
,因为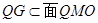
所以QG//平面PBC.
考点:线面垂直,线面平行,面面平行

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 ,点
,点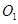 为
为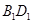 的中点.
的中点.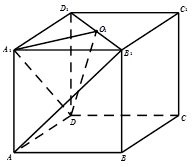
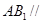 面
面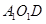 ;
;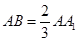 ,试问在线段
,试问在线段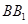 上是否存在点
上是否存在点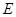 使得
使得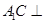
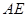 ,若存在求出
,若存在求出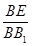 ,若不存在,说明理由.
,若不存在,说明理由.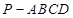 中,底面
中,底面 是直角梯形,
是直角梯形,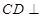 平面
平面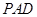 ,
,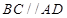 ,
,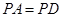 ,
,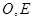 分别为
分别为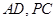 的中点,
的中点,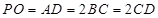 .
.
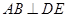 ;
; 的余弦值.
的余弦值.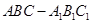 中,侧面
中,侧面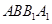 为矩形,
为矩形,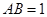 ,
,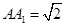 ,
, 为
为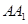 的中点,
的中点,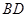 与
与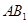 交于点
交于点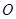 ,
,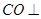 侧面
侧面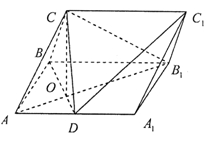
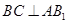 ;
;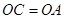 ,求直线
,求直线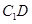 与平面
与平面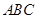 所成角的正弦值.
所成角的正弦值.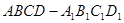 中,
中,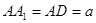 ,
,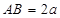 ,
,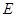 、
、  分别为
分别为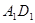 、
、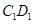 的中点.
的中点.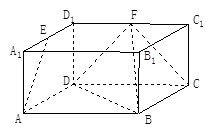
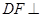 平面
平面 ;
;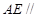 平面
平面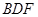 .
.
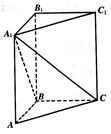
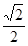 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.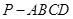 中,
中,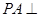 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,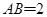 ,
,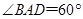 .
.
 平面PAC;
平面PAC;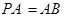 ,求
,求 与
与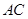 所成角的余弦值;
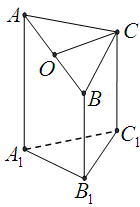
所成角的余弦值;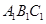 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为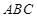 .已知
.已知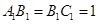 ,
,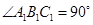 ,
,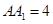 ,
,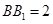 ,
,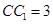 .
.
 是
是 的中点,证明:
的中点,证明: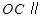 平面
平面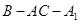 的大小;
的大小;