题目内容
(本小题满分14分)
已知椭圆的中心在坐标原点 ,长轴长为
,长轴长为 ,离心率
,离心率 ,过右焦点
,过右焦点 的直线
的直线 交椭圆于
交椭圆于 ,
, 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)当直线 的斜率为1时,求
的斜率为1时,求 的面积;
的面积;
(Ⅲ)若以 为邻边的平行四边形是矩形,求满足该条件的直线
为邻边的平行四边形是矩形,求满足该条件的直线 的方程.
的方程.
(1) ,(2)
,(2) (3)
(3)
【解析】
试题分析:(Ⅰ)由已知,椭圆方程可设为 .
.
∵长轴长为 ,离心率
,离心率 ,∴
,∴ .
.
所求椭圆方程为 .
.
(Ⅱ)因为直线 过椭圆右焦点
过椭圆右焦点 ,且斜率为
,且斜率为 ,所以直线
,所以直线 的方程为
的方程为 .
.
设 ,
,
由  得
得  ,解得
,解得  .
.
∴  .
.
(Ⅲ)当直线 与
与 轴垂直时,直线
轴垂直时,直线 的方程为
的方程为 ,此时
,此时 小于
小于 ,
, 为邻边的平行四边形不可能是矩形.
为邻边的平行四边形不可能是矩形.
当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为 .
.
由  可得
可得 .
.
∴ .
. ,
,
 因为以
因为以 为邻边的平行四边形是矩形
为邻边的平行四边形是矩形 .
.
由 得
得 ,
,
 .
. 所求直线的方程为
所求直线的方程为 .
.
考点:本题考查直线与椭圆的位置关系
点评:由已知条件可直接得到a,b,求出椭圆方程,求三角形面积要先用弦长公式,求出弦长,平行四边形为矩形,用向量点乘积为0,算出k

练习册系列答案
相关题目
 ,则
,则 ,
, ,
, 的大小关系是
的大小关系是 B.
B. 
 D.
D. 
 的圆心位于第二象限且在直线
的圆心位于第二象限且在直线 上,若圆
上,若圆 的值是
的值是
 ,那么
,那么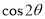 的值等于 .
的值等于 .
 在不等式组
在不等式组 表示的平面区域内,则点
表示的平面区域内,则点 到直线
到直线 距离的最大值为( )
距离的最大值为( ) (B)
(B) (C)
(C) (D)8
(D)8 中,E是棱BC上的一点,则三棱锥
中,E是棱BC上的一点,则三棱锥 的体积等于( )
的体积等于( )
 B.
B. C.
C. D.
D.
 )上是减函数的是
)上是减函数的是 B.
B. C.
C. D.
D.