题目内容
【题目】(1)若动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() :
:![]() 的距离之比为
的距离之比为![]() ,求证:动点
,求证:动点![]() 的轨迹是椭圆;
的轨迹是椭圆;
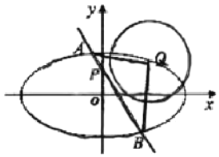
(2)设(1)中的椭圆短轴的上顶点为![]() ,试找出一个以点
,试找出一个以点![]() 为直角顶点的等腰直角三角形
为直角顶点的等腰直角三角形![]() ,并使得
,并使得![]() 、
、![]() 两点也在椭圆上,并求出
两点也在椭圆上,并求出![]() 的面积;
的面积;
(3)对于椭圆![]() (常数
(常数![]() ),设椭圆短轴的上顶点为
),设椭圆短轴的上顶点为![]() ,试问:以点
,试问:以点![]() 为直角顶点,且
为直角顶点,且![]() 、
、![]() 两点也在椭圆上的等腰直角三角形
两点也在椭圆上的等腰直角三角形![]() 有几个?
有几个?
【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】
(1)假设动点![]() 坐标,利用条件,建立等式,化简可判断动点
坐标,利用条件,建立等式,化简可判断动点![]() 的轨迹;
的轨迹;
(2)根据条件可知,![]() ,
,![]() 应是关于
应是关于![]() 轴对称,将直线方程与椭圆方程联立,从而可求
轴对称,将直线方程与椭圆方程联立,从而可求![]() 长,故可求面积;
长,故可求面积;
(3)与(2)相同的求法,将直线方程与椭圆方程联立,求![]() ,
,![]() 的长,利用
的长,利用![]() 即可得出答案.
即可得出答案.
(1)![]() 动点
动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() :
:![]() 的距离之比为
的距离之比为![]()
![]()
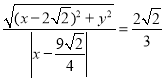 ,化简可得:
,化简可得:![]() ,
,![]() 动点
动点![]() 的轨迹是椭圆.
的轨迹是椭圆.
(2)![]() 椭圆方程为
椭圆方程为![]() ,
,![]()
又![]() 等腰直角三角形
等腰直角三角形![]() 是以
是以![]() 为直角顶点,
为直角顶点,
不妨设![]() 点在
点在![]() 轴左侧,则
轴左侧,则![]() 点在
点在![]() 轴右侧,
轴右侧,
若直线![]() 、
、![]() 关于
关于![]() 轴对称且该三角形为等腰直角三角形,可取
轴对称且该三角形为等腰直角三角形,可取![]() ,则
,则![]() ,
,
![]()
![]() ,
,![]() ,
,
联立椭圆方程和![]() 直线方程可得:
直线方程可得: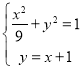 ,
,
消掉![]() :可得:
:可得:![]() ,解得
,解得![]()
![]()
![]() 故
故![]() ,可得
,可得![]()
根据两点间距离公式可得:

![]() 等腰直角三角形
等腰直角三角形![]() 是以
是以![]() 、
、![]() 为直角边,
为直角边,
![]()
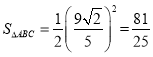 ;
;
(3)![]() 椭圆方程为
椭圆方程为![]() ,
,![]() ,设
,设![]() ,
,
联立椭圆方程和![]() 直线方程可得:
直线方程可得: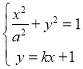 ,
,
消掉![]() 可得:
可得:![]() ,
,![]() 解得
解得![]()
![]() ,
,
又![]() 根据弦长公式可得:
根据弦长公式可得:![]() ,
,
同理可得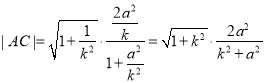 ,
,
![]()
![]() ,
,![]()
![]() ,
,
化简可得:![]() ,即:
,即:![]() ,
,
可得![]() 或
或![]()
当![]() 且
且![]() ,即
,即![]() 时,
时,![]() 有三个解,即这样的三角形有
有三个解,即这样的三角形有![]() 个;
个;
当![]() 时,即当
时,即当![]() 时,方程
时,方程![]() 为
为![]() ,解得
,解得![]() ,这样的三角形只有
,这样的三角形只有![]() 个;
个;
当![]() 时,即当
时,即当![]() 时,
时,![]() 只有一个解,即这样的三角形有
只有一个解,即这样的三角形有![]() 个.
个.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目