题目内容
在数列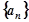 中,已知
中,已知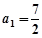 ,
,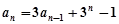 (
(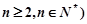 .
.
(1)求证: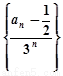 是等差数列;
是等差数列;
(2)求数列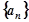 的通项公式
的通项公式 及它的前
及它的前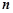 项和
项和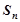 .
.
【答案】
(1)见解析(2)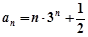 ,
,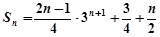
【解析】本试题主要是考查了等差数列的定义以及错位相减法的求和的综合运用。
(1)根据已知的递推关系式,得到数列的相邻两项的关系式,进而结合定义证明。
(2)在第一问的基础上,得到数列的通项公式,然后借助于错位相减法得到结论。
(1)证明:∵ 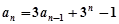 (
(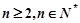 )
)
∴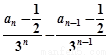
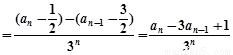
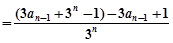
 为常数
为常数
∴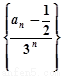 是等差数列,且公差为1.
…………………… 5分
是等差数列,且公差为1.
…………………… 5分
(2)解:由(1)知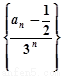 是等差数列,且公差为1,且
是等差数列,且公差为1,且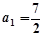
∴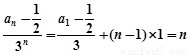 ∴
∴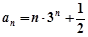 …………… 8分
…………… 8分
∴  ……………
9分
……………
9分
令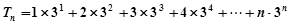 …………①
…………①
则 ……②…………… 10分
……②…………… 10分
两式相减得:
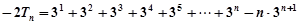 ……………… 11分
……………… 11分

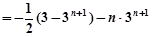 …………… 12分
…………… 12分
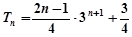 ………………… 13分
………………… 13分
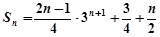 ………………… 14分
………………… 14分

练习册系列答案
相关题目
 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 .
.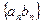 的前
的前 项和
项和 中,已知:
中,已知: .
.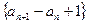 是
是 等比数列.
等比数列. .
.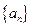 中,已知
中,已知
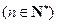 .
. 项和
项和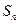 .
. 中,已知
中,已知 且
且 。
。 证明:数列
证明:数列 是等差数列,并求数列
是等差数列,并求数列 求
求 的值。
的值。 中,已知
中,已知 ,
, .
.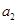 、
、 并判断
并判断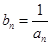 ,求证:
,求证: 为等比数列;
为等比数列;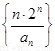 的前n项和
的前n项和 .
.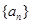 中,已知
中,已知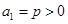 ,且
,且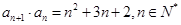 .
.