题目内容
已知x∈R,m∈R,比较x2+x+1与-2m2+2mx的大小.
思路分析:在这里,作差后无法进行因式分解而转化为积的形式,注意到这里有两个字母x和m,因此我们要对它们进行配方,把它们转化为非负实数之和,从而确定其符号.
解:∵x2+x+1-(-2m2+2mx)=x2-(2m-1)x+2m2+1
=(x-m+
)2+m2+m+
=(x-m+
)2+(m+
)2+
＞0,
∴x2+x+1＞-2m2+2mx.
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
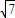tanθ）x+1，
）+
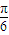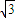sin（2x+
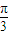）时，g（x）在A上是单调递减函数，求θ的取值范围．
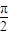，0）对称，又关于直线x=π成轴对称，试探讨ω应该满足的条件．