题目内容
圆心是C（-2，1），且过点M（2，-2）的圆的方程是 ．
分析：根据题意，设圆的标准方程为（x+2）2+（y-1）2=r2，代入点M的坐标解出r2=25，即可得到所求圆的方程．
解答：解：∵圆心是C（-2，1），∴设圆的方程为（x+2）2+（y-1）2=r2，
又∵点M（2，-2）在圆上，
∴（2+2）2+（-2-1）2=r2，解得r2=25．
由此可得所求圆的方程为（x+2）2+（y-1）2=25．
故答案为：（x+2）2+（y-1）2=25
又∵点M（2，-2）在圆上，
∴（2+2）2+（-2-1）2=r2，解得r2=25．
由此可得所求圆的方程为（x+2）2+（y-1）2=25．
故答案为：（x+2）2+（y-1）2=25
点评：本题给出以定点C为圆心且经过定点M的圆，求圆的方程．考查了圆的标准方程及其应用的知识，属于基础题．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
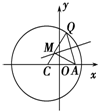设圆（x+1）2+y2=25的圆心为C，A（1，0）是圆内一定点，Q为圆周上任一点．线段AQ的垂直平分线与CQ的连线交于点M，则M的轨迹方程为（ ）