题目内容
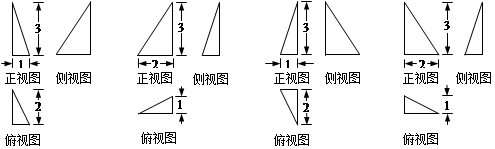
一个几何体的三视图如右图所示，则该几何体的体积为（ ）
A． | B． | C． | D． |
A
解析试题分析：由三视图可知该几何体，是过一正三棱柱的上底面一边作截面，截去的部分为三棱锥，利用间接法求出其体积。解：由三视图可知该几何体，是过一正三棱柱的上底面一边作截面，截去的部分为三棱锥，而得到的几何体．原正三棱锥的底面边长为2，高为2，体积V1=Sh=
×2×
×2=2截去的三棱锥的高为1，体积V2=
×1=
故所求体积为V=V1-V2=
故选A
考点：三视图求几何体的体积
点评：本题考查三视图求几何体的体积，考查计算能力，空间想象能力，三视图复原几何体是解题的关键
练习册系列答案
阅读快车系列答案
相关题目
三棱锥
的四个顶点都在体积为
的球的表面上，底面ABC所在的小圆面积为16π，则该三棱锥的高的最大值为( )
| A．7 | B．7.5 | C．8 | D．9 |
长为2；侧视图一直角三角形；俯视图为一直角梯形，且
,则此几何体的体积是（ ）。
某个几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的表面积是（ ）
A． | B． |
C．6+ | D． |
棱长都是1的三棱锥的表面积为（ ）
A． | B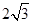． | C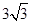． | D． |
一个三棱锥的三视图如图所示，则该几何体的表面积为（ ）
A． | B． |
C． | D．8 |
若某空间几何体的三视图如图所示，则该几何体的体积是（ ）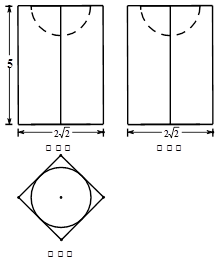
| A．20-2π | B． | C． | D． |
三棱锥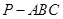
中，
，
， 
⊥底面
，且
，则此三棱锥外接球的半径为
A． | B． | C．2 | D． |