题目内容
(请在答题卡上答题)
已知 ,函数
,函数 ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).
(1)讨论函数 在
在 上的单调性;
上的单调性;
(2)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直? 若存在,求出
轴垂直? 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若实数 满足
满足 ,求证:
,求证: .
.
【答案】
解(1)∵ ,
, ,∴
,∴ .
.
若 ,则
,则 ,
, 在
在 上单调递增;
上单调递增;
① ②若 ,当
,当 时,
时, ,函数
,函数 在区间
在区间 上单调递减,
上单调递减,
当 时,
时, ,函数
,函数 在区间
在区间 上单调递增,
上单调递增,
③若 ,则
,则 ,函数
,函数 在区间
在区间 上单调递减.
上单调递减.
(2)解:∵ ,
, ,
,

 ,
,
由(1)易知,当 时,
时, 在
在 上的最小值:
上的最小值: ,即
,即 时,
时, .
.
又 ,∴
,∴ .
.
曲线 在点
在点 处的切线与
处的切线与 轴垂直等价于方程
轴垂直等价于方程 有实数解.
有实数解.
而 ,即方程
,即方程 无实数解.故不存在.
无实数解.故不存在.
(3)证明:



 ,由(2)知
,由(2)知 ,令
,令 得
得 .
.

练习册系列答案
相关题目
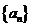 满足
满足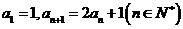
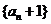 是等比数列;
是等比数列;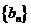 满足
满足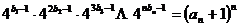 ,求数列
,求数列 ,求数列
,求数列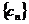 的前n项和
的前n项和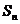 .
. 如图,已知正三棱柱
如图,已知正三棱柱 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是 的中点,直线
的中点,直线 与侧面
与侧面 所成的角是
所成的角是 .
. 的大小;
的大小; 到平面
到平面 的距离.
的距离. 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为 元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元,假设座位等距离分布,且至少有四个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元. 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低? 分,一名观众随意连线,将他的得分记作ξ.
分,一名观众随意连线,将他的得分记作ξ. 中,在,
中,在, 分别是角
分别是角 所对的边,
所对的边, ,试判断
,试判断