题目内容
设 1=a1≤a2≤…≤a7,其中a1,a3,a5,a7 成公比为q的等比数列,a2,a4,a6 成公差为1的等差数列,则q的最小值是 .
【答案】分析:利用等差数列的通项公式将a6用a2表示,求出a6的最小值进一步求出a7的最小值,利用等比数列的通项求出公比的范围.
解答:解:方法1:∵1=a1≤a2≤…≤a7; a2,a4,a6 成公差为1的等差数列,
∴a6=a2+2≥3,
∴a6的最小值为3,
∴a7的最小值也为3,
此时a1=1且a1,a3,a5,a7 成公比为q的等比数列,必有q>0,
∴a7=a1q3≥3,
∴q3≥3,q≥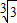 ,
,
方法2:
由题意知1=a1≤a2≤…≤a7;中a1,a3,a5,a7 成公比为q的等比数列,a2,a4,a6 成公差为1的等差数列,得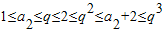 ,所以
,所以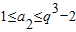 ,即q3-2≥1,所以q3≥3,解得q≥
,即q3-2≥1,所以q3≥3,解得q≥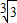 ,
,
故q的最小值是: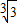 .
.
故答案为: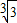 .
.
点评:解决等差数列、等比数列的综合问题一般利用通项公式、前n项和公式列出方程组,解方程组求解.即基本量法.
解答:解:方法1:∵1=a1≤a2≤…≤a7; a2,a4,a6 成公差为1的等差数列,
∴a6=a2+2≥3,
∴a6的最小值为3,
∴a7的最小值也为3,
此时a1=1且a1,a3,a5,a7 成公比为q的等比数列,必有q>0,
∴a7=a1q3≥3,
∴q3≥3,q≥
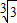 ,
,方法2:
由题意知1=a1≤a2≤…≤a7;中a1,a3,a5,a7 成公比为q的等比数列,a2,a4,a6 成公差为1的等差数列,得
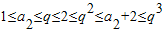 ,所以
,所以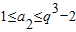 ,即q3-2≥1,所以q3≥3,解得q≥
,即q3-2≥1,所以q3≥3,解得q≥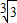 ,
,故q的最小值是:
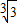 .
.故答案为:
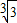 .
.点评:解决等差数列、等比数列的综合问题一般利用通项公式、前n项和公式列出方程组,解方程组求解.即基本量法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目