题目内容
(本题满分15分)如图,已知长方形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)求证:![]()
(2)点![]() 是线段
是线段![]() 上的一动点,当二面角
上的一动点,当二面角![]() 大小为
大小为![]() 时,试确定点
时,试确定点![]() 的位置.
的位置.


(本题满分15分)
解法一 (1)由于![]() ,则
,则![]() ,……………………2分
,……………………2分
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() =
=![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() . ………………………4分
. ………………………4分
又![]() 平面
平面![]() ,从而有
,从而有![]() . ………………………8分
. ………………………8分
(2)过点E作MB的平行线交DM于F,由![]() 平面
平面![]() 得
得![]() 平面ADM; 在平面ADM中过点F作AM的垂线,垂足为H,连接HE,则
平面ADM; 在平面ADM中过点F作AM的垂线,垂足为H,连接HE,则![]() 即为二面角
即为二面角![]() 的
的
 平面角,为
平面角,为![]() . …………………………………………………………11分
. …………………………………………………………11分
设![]() ,则
,则![]() 在
在![]() 中,
中,
由![]() ,则
,则![]() .
.
由 .
.
………………………………13分
故当E位于线段DB间,且![]() 时,二面角
时,二面角![]() 大小为
大小为![]()
………………………………15分
解法二.取AM的中点O,AB的中点B,则![]() 两两垂直,以O为原点建立空间直角坐标系,如图.根据已知条件,得
两两垂直,以O为原点建立空间直角坐标系,如图.根据已知条件,得
![]() ,
,![]() ,
,![]() ,
,![]() ………2分
………2分
 (1)由于
(1)由于![]() ,……………………………………4分
,……………………………………4分
则![]() ,故
,故![]() .……………………6分
.……………………6分
(2)设存在满足条件的点E,并设![]() ,
,
则![]()
则点E的坐标为![]() .(其中
.(其中![]() )……………………8分
)……………………8分
易得平面ADM的法向量可以取![]() ,……………………………………9分
,……………………………………9分
设平面AME的法向量为![]() ,则
,则![]() ,
,
![]()
则
则![]() ,取
,取![]() …………11分
…………11分
由于二面角![]() 大小为
大小为![]() ,则
,则 
![]() ,由于
,由于![]() ,故解得
,故解得![]() .………………13分
.………………13分
故当E位于线段DB间,且![]() 时,二面角
时,二面角![]() 大小为
大小为![]()
……………………15分


 中,底面
中,底面 是矩形,
是矩形, 平面
平面 与平面
与平面 和
和 ,
, ,
, 依次是
依次是 的中点.
的中点. ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 沿直线EF将
沿直线EF将 翻折成
翻折成 使平面
使平面 平面BEF.
平面BEF. 的余弦值;
的余弦值;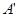 重合,求线段FM的长.
重合,求线段FM的长.
 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 的中点,
的中点, 分别落在线段
分别落在线段 上.已知
上.已知 米,
米, 米,记
米,记 .
. 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
 本题满分15分)如图, 在矩形
本题满分15分)如图, 在矩形 中,点
中,点 分别
分别 上,
上, .沿直线
.沿直线
 翻折成
翻折成 ,使平面
,使平面 .
.
 的余弦值;
的余弦值; 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段