题目内容
(08年四校联考二理) 已知数列![]() 满足
满足![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求证:![]() 对于
对于![]() 恒成立;
恒成立;
(Ⅱ)求数列![]() 的通项公式
的通项公式![]() ;
;
(Ⅲ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .求证:对任意的
.求证:对任意的![]() ,
,![]() .
.
解析:(Ⅰ)若![]() (
(![]() ),则由
),则由![]() 知
知![]() ,依次类推可知进而
,依次类推可知进而![]() ,这与
,这与![]() 矛盾.所以,
矛盾.所以,![]() (
(![]() ).
).
又![]() ,所以,
,所以,![]() 对于
对于![]() 恒成立.
恒成立.
(Ⅱ)在![]() 两边同除以
两边同除以![]() ,并移项有
,并移项有
![]() ,
,
于是,![]() ,
,
![]() 数列
数列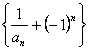 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
![]() , 即
, 即![]() .
.
(Ⅲ)![]() ,
,![]() .
.
当![]() 时,则
时,则![]()
![]()
![]()
![]() .又易知
.又易知![]() ,
,

练习册系列答案
相关题目

