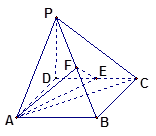
题目内容
如图,已知 ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,且
,且 是
是 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证:平面BCE⊥平面 ;
;
(III) 求此 多面体的体积.
多面体的体积.

 ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,且
,且 是
是 的中点.
的中点.
(Ⅰ)求证:
 ∥平面
∥平面 ;
;(Ⅱ)求证:平面BCE⊥平面
 ;
;(III) 求此
 多面体的体积.
多面体的体积.
解:(Ⅰ)取 CE中点P,连结FP、BP,
CE中点P,连结FP、BP,
∵F为CD的中点, ∴FP∥DE,且FP=
又AB∥DE,且AB= ∴AB∥FP,且AB=FP,
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,∴AF∥BP. …………3分
又∵AF 平面BCE,BP
平面BCE,BP ∴AF∥平面BCE …………4分
∴AF∥平面BCE …………4分
(Ⅱ)∵ ,所以△ACD为正三角形,∴AF⊥CD
,所以△ACD为正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE//AB ∴DE⊥平面ACD 又AF 平面ACD
平面ACD
∴DE⊥AF 又AF⊥CD,CD∩DE=D
∴AF⊥平面CDE 又BP∥AF ∴BP⊥平面CDE
又∵BP 平面BCE ∴平面BCE⊥平面CDE …………8分
平面BCE ∴平面BCE⊥平面CDE …………8分
(III)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,
 ,
, 等边三角形AD边上的高就是四棱锥的高
等边三角形AD边上的高就是四棱锥的高


 CE中点P,连结FP、BP,
CE中点P,连结FP、BP,∵F为CD的中点, ∴FP∥DE,且FP=

又AB∥DE,且AB=
 ∴AB∥FP,且AB=FP,
∴AB∥FP,且AB=FP,∴ABPF为平行四边形,∴AF∥BP. …………3分
又∵AF
 平面BCE,BP
平面BCE,BP ∴AF∥平面BCE …………4分
∴AF∥平面BCE …………4分(Ⅱ)∵
 ,所以△ACD为正三角形,∴AF⊥CD
,所以△ACD为正三角形,∴AF⊥CD∵AB⊥平面ACD,DE//AB ∴DE⊥平面ACD 又AF
 平面ACD
平面ACD∴DE⊥AF 又AF⊥CD,CD∩DE=D
∴AF⊥平面CDE 又BP∥AF ∴BP⊥平面CDE
又∵BP
 平面BCE ∴平面BCE⊥平面CDE …………8分
平面BCE ∴平面BCE⊥平面CDE …………8分(III)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,
 ,
, 等边三角形AD边上的高就是四棱锥的高
等边三角形AD边上的高就是四棱锥的高

略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
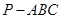 中,
中,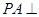 底面ABC
底面ABC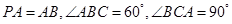 ,点
,点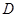 、
、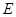 分别在棱
分别在棱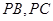 上,且
上,且
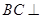 平面
平面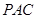 ;
;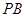 的中点时,求
的中点时,求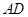 与平面
与平面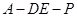 为直二面角?并说明理由.
为直二面角?并说明理由.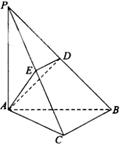
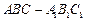
 中,已知
中,已知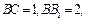
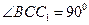 ,
,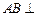 侧面
侧面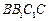 .
.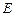 为棱
为棱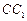 的中点,
的中点,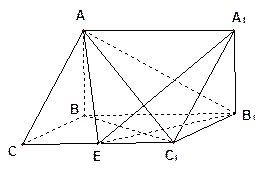
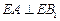 ;(2)若
;(2)若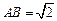 ,求二面角
,求二面角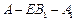 的大小.
的大小.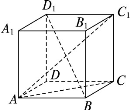
 是边长为1的正方体,求:
是边长为1的正方体,求:
 与平面
与平面 所成角的正切值;
所成角的正切值; 的大小;
的大小; 到平面
到平面 的距离。
的距离。 ,AA1=4,点D是AB的中点
,AA1=4,点D是AB的中点 的平面角的正切值
的平面角的正切值 B
B  C
C  D 都不对
D 都不对 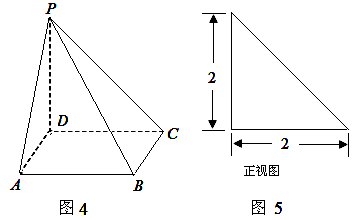
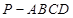 中,底面ABCD为矩形,
中,底面ABCD为矩形,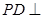 底面ABCD,AD=PD=1,AB=
底面ABCD,AD=PD=1,AB=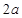 (
(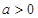 ),E,F分别CD,PB的中点。
),E,F分别CD,PB的中点。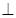 平面PAB;,
平面PAB;,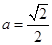 时,求AC与平面AEF所成角的正弦值。
时,求AC与平面AEF所成角的正弦值。