题目内容
若x2+（x+1）7=a0+a1（x+2）+a2（x+2）2+…+a7（x+2）7，则a2=（ ）
| A、20 | B、19 |
| C、-20 | D、-19 |
考点：二项式系数的性质
专题：二项式定理
分析：由题意可得[-2+（x+2）]2+[-1+（x+2）]7=a0+a1（x+2）+a2（x+2）2+…+a7（x+2）7，可得a2=
+
•（-1）5，计算求得结果．
| C | 2 2 |
| C | 2 7 |
解答：
解：x2+（x+1）7=[-2+（x+2）]2+[-1+（x+2）]7=a0+a1（x+2）+a2（x+2）2+…+a7（x+2）7．
∴a2=
+
•（-1）5=-20，
故选：C．
∴a2=
| C | 2 2 |
| C | 2 7 |
故选：C．
点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
相关题目
有五条线段长度分别为1，3，5，7，9，从这5条线段中任取3条，则所取3条线段能构成一个锐角三角形的概率为（ ）
A、
| ||
B、
| ||
| C、0 | ||
D、
|
要得到函数y=cosx的图象，只需将函数y=cos（x+
）的图象沿x轴（ ）
| π |
| 4 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
方程y=k（x-2）表示（ ）
| A、过点（-2，0）的一切直线 |
| B、过点（2，0）的一切直线 |
| C、过点（2，0）且不垂直于x轴的一切直线 |
| D、过点（2，0）且除去x轴的一切直线 |
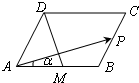在平行四边形ABCD中，AB=2，AD=1，∠DAB=60°，点M为AB的中点，点P从B→C→D（含端点），设∠PAB=α，记tanα=x，| AP |
| DM |
A、 |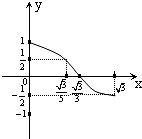
B、 |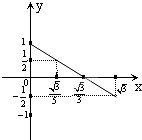
C、 |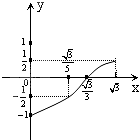
D、 |
在△ABC中，角A，B，C所对的边分别为a，b，c，a=1，B=45°，S△ABC=2，则△ABC的外接圆半径为（ ）
A、2
| ||||
B、3
| ||||
C、
| ||||
D、
|
在△ABC中，A=60°，b=1，且面积为
，则
=（ ）
| 3 |
| 2a+2b-2c |
| sinA+sinB-sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、4
|
在回归模型中，预报变量的值与下列哪些因素有关（ ）
| A、受解释变量的影响与随机误差无关 |
| B、受随机误差的影响与解释变量无关 |
| C、与总偏差平方和有关与残差无关 |
| D、与解释变量和随机误差的总效应有关 |