题目内容
已知点 在由不等式组
在由不等式组 确定的平面区域内,则
确定的平面区域内,则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
D
解析试题分析: 因为根据题意,点 在由不等式组
在由不等式组 确定的平面区域内,作出可行域,如下图,设w=
确定的平面区域内,作出可行域,如下图,设w= =
= =4+2×
=4+2×

作出可行域,分析可得:
点(a,b)与点(-3,-2)确定的直线的
斜率为[ ,
, ]从而可以求得w的取值范围为[
]从而可以求得w的取值范围为[ ,
, ]
]
则 的最大值为
的最大值为 故选D
故选D
考点:本题主要考查了画不等式组表示的平面区域,利用两点连线的斜率公式给目标函数赋予几何意义,数形结合求出范围
点评:解决该试题的关键是画出可行域,将目标函数变形,赋予几何意义,是可行域中的点与点(-3,-2)连线的斜率的2倍加上4,由图求出取值范围。

练习册系列答案
相关题目
若 的取值范围是( )
的取值范围是( )
| A.[3,5] | B.[2,5] | C.[3,6] | D.[2,6] |
在平面直角坐标系中,已知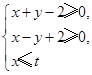 若目标函数
若目标函数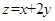 的最大值是10,则实数
的最大值是10,则实数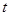 的值为
的值为
| A.1 | B.2 | C.3 | D.4 |
满足线性约束条件 的目标函数
的目标函数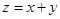 的最大值是( )
的最大值是( )
| A.1 | B.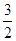 | C.2 | D.3 |
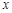 、
、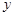 满足约束条件:
满足约束条件: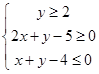 ,则
,则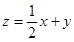 的最小值是
的最小值是
| A.2 | B.3 | C.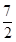 | D.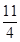 |
设变量 满足约束条件
满足约束条件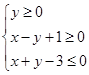 ,则
,则 的最大值为 ( )
的最大值为 ( )
| A.—2 | B.4 | C.6 | D.8 |
在下列各点中,不在不等式 表示的平面区域内的点为( )
表示的平面区域内的点为( )
A.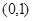 | B.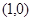 | C.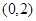 | D.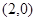 |
下列给出的四个点中,位于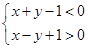 表示的平面区域内的点是 ( )
表示的平面区域内的点是 ( )
A.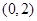 | B.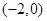 | C.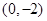 | D.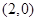 |
设 满足约束条件
满足约束条件 ,则
,则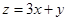 的最大值为 ( )
的最大值为 ( )
| A.5 | B.3 | C.7 | D.-8 |