题目内容
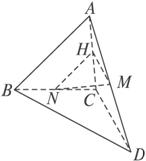
空间四边形ABCD中,M、N分别为AD、BC的中点,求证:AB+CD＞2MN.
证明:取AC的中点H,连结NH、MH.
∵M、N分别为AD、BC的中点,
∴NH=
AB,MH=
CD.
又NH+MH＞MN,
∴
(AB+CD)＞MN,
即AB+CD＞2MN.
练习册系列答案
相关题目
题目内容
空间四边形ABCD中,M、N分别为AD、BC的中点,求证:AB+CD＞2MN.
证明:取AC的中点H,连结NH、MH.
∵M、N分别为AD、BC的中点,
∴NH=AB,MH=CD.
又NH+MH＞MN,
∴(AB+CD)＞MN,
即AB+CD＞2MN.
如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
如图，空间四边形ABCD中，AB、BC、CD的中点分别是P、Q、R，且