题目内容
设抛物线 上与点A(6,0)距离最近的点为N,点N的纵坐标与横坐标的差为c。已知函数f(x)=ax3+bx2-3x+c在x=±1处取得极值。
上与点A(6,0)距离最近的点为N,点N的纵坐标与横坐标的差为c。已知函数f(x)=ax3+bx2-3x+c在x=±1处取得极值。
(1)讨论f(1)和f(-1)是函数f(x)的极大值还是极小值;
(2)过点P(0,16)作y=f(x)的切线,求此切线的方程。
 上与点A(6,0)距离最近的点为N,点N的纵坐标与横坐标的差为c。已知函数f(x)=ax3+bx2-3x+c在x=±1处取得极值。
上与点A(6,0)距离最近的点为N,点N的纵坐标与横坐标的差为c。已知函数f(x)=ax3+bx2-3x+c在x=±1处取得极值。(1)讨论f(1)和f(-1)是函数f(x)的极大值还是极小值;
(2)过点P(0,16)作y=f(x)的切线,求此切线的方程。
解:(1)设N(x,y)为抛物线 上一点,则
上一点,则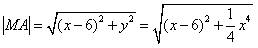 ,
,
|MA|与|MA|2同时取到极值,
令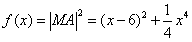 ,
,
由 得x=2,
得x=2,
而当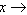 +∞或
+∞或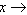 -∞时,
-∞时,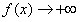 ,
,
∴ 此时x=2,y=2,
此时x=2,y=2,
即抛物线上与点A(6,0)距离最近的点N(2,2),
∴c=0,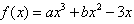 ,
,
∴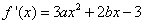 ,
,
依题意,得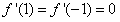 ,
,
即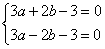 ,解得:
,解得: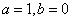 ,
,
∴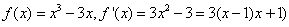 ,
,
令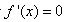 ,得x=1或x=-1;
,得x=1或x=-1;
若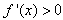 ,得x>1或x<1;
,得x>1或x<1;
若 ,得-1<x<1,
,得-1<x<1,
所以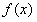 在(-∞,-1)上是增函数,在(1,+∞)上是增函数,在(-1,1)上是减函数,
在(-∞,-1)上是增函数,在(1,+∞)上是增函数,在(-1,1)上是减函数,
(2)曲线方程为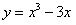 ,点P(0,16)不在曲线上,
,点P(0,16)不在曲线上,
设切点Q(x0,y0),则点Q的坐标满足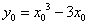 ,
,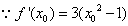 ,
,
故切线的方程为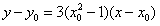 ,
,
因为点P在切线上,
∴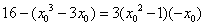 ,
,
化简,得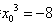 ,解得:
,解得: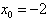 ,
,
所以,切点为Q(-2,-2),
所以切线的方程为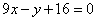 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.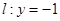 相切,设圆心C的轨迹为曲线E,A、B(A在y轴的右侧)为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B(A在y轴的右侧)为曲线E上的两点,点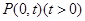 ,且满足
,且满足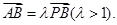
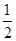 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;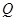 ,若点
,若点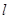 上,求证:t与
上,求证:t与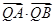 均为定值.
均为定值.