题目内容
若圆C过点M(0,1)且与直线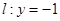 相切,设圆心C的轨迹为曲线E,A、B(A在y轴的右侧)为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B(A在y轴的右侧)为曲线E上的两点,点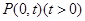 ,且满足
,且满足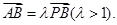
(Ⅰ)求曲线E的方程;
(Ⅱ)若t=6,直线AB的斜率为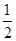 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
(Ⅲ)分别过A、B作曲线E的切线,两条切线交于点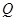 ,若点
,若点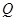 恰好在直线
恰好在直线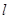 上,求证:t与
上,求证:t与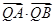 均为定值.
均为定值.
【答案】
(Ⅰ) .(Ⅱ)
.(Ⅱ) .(Ⅲ)t与
.(Ⅲ)t与 均为定值.
均为定值.
【解析】(I)由于圆心C到定点M的距离与到定直线y=-1的距离相等,所以其轨迹为抛物线其方程为 .
.
(II)因为t=6,所以直线AB的斜率为 ,直线AB的方程是
,直线AB的方程是 .然后与抛物线方程联立求出A、B的坐标.再利用导数求出点A处的切线的斜率,进而确定NA的斜率,求出NA的方程.再求出AB的垂直平分线方程与NA的方程联立,可求出圆心N的坐标,进而可求出半径的值,写出圆N的方程.
.然后与抛物线方程联立求出A、B的坐标.再利用导数求出点A处的切线的斜率,进而确定NA的斜率,求出NA的方程.再求出AB的垂直平分线方程与NA的方程联立,可求出圆心N的坐标,进而可求出半径的值,写出圆N的方程.
(III) 设 ,由题意可知
,由题意可知 ,从而可知
,从而可知 是方程
是方程 即
即 的两根,得到
的两根,得到 ,
,
再根据A,P,B共线,斜率相等可求出t的值.
然后根据
 可证明
可证明 也为定值
也为定值

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
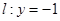 相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点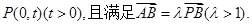
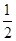 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;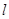 上,求证:t与
上,求证:t与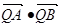 均为定值。
均为定值。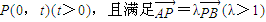 .
. ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;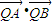 均为定值.
均为定值.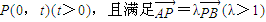 .
. ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;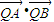 均为定值.
均为定值.