题目内容
已知函数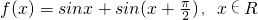 .
.
( I) 求f(x)的最小正周期T
( II) 求f(x)的最大值和最小值,并分别写出使f(x)取最大值和最小值时的x的集合.
( III) 用“五点法”作出函数在一个周期内的简图.
解: …..(2分)
…..(2分)
(Ⅰ)f(x)的最小正周期为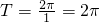 …(4分)
…(4分)
(Ⅱ)f(x)的最大值为 ,此时x+
,此时x+ =2kπ+
=2kπ+ ,k∈Z,x的取值集合是
,k∈Z,x的取值集合是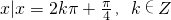 ….(6分)f(x)的最小值
….(6分)f(x)的最小值 ,此时x+
,此时x+ =2kπ-
=2kπ- ,k∈Z,x的取值 x的取值集合是
,k∈Z,x的取值 x的取值集合是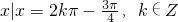 …..(8分)
…..(8分)
(Ⅲ)列表:
描点连线得出图象.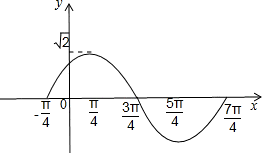
分析:利用三角函数公式将f(x)化成一角一函数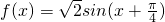 后,
后,
( I) 利用三角函数求周期公式求解
(Ⅱ)利用三角函数性质求出最值及最值点.
(Ⅲ)将x+ 看作整体,令x+
看作整体,令x+ 取0,
取0,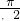 ,π,
,π, ,2π,并求出对应的x的值,列表,用五点画图法画出函数图象即可.
,2π,并求出对应的x的值,列表,用五点画图法画出函数图象即可.
点评:本题考查诱导公式的应用,三角函数性质、五点法作图,考查了整体思想和作图能力.
 …..(2分)
…..(2分)(Ⅰ)f(x)的最小正周期为
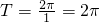 …(4分)
…(4分)(Ⅱ)f(x)的最大值为
 ,此时x+
,此时x+ =2kπ+
=2kπ+ ,k∈Z,x的取值集合是
,k∈Z,x的取值集合是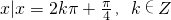 ….(6分)f(x)的最小值
….(6分)f(x)的最小值 ,此时x+
,此时x+ =2kπ-
=2kπ- ,k∈Z,x的取值 x的取值集合是
,k∈Z,x的取值 x的取值集合是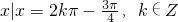 …..(8分)
…..(8分)(Ⅲ)列表:
x+ | 0 |  | π |  | 2π |
| x | - |  |  |  |  |
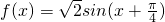 | 0 |  | 0 | - | 0 |

分析:利用三角函数公式将f(x)化成一角一函数
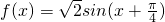 后,
后,( I) 利用三角函数求周期公式求解
(Ⅱ)利用三角函数性质求出最值及最值点.
(Ⅲ)将x+
 看作整体,令x+
看作整体,令x+ 取0,
取0,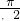 ,π,
,π, ,2π,并求出对应的x的值,列表,用五点画图法画出函数图象即可.
,2π,并求出对应的x的值,列表,用五点画图法画出函数图象即可.点评:本题考查诱导公式的应用,三角函数性质、五点法作图,考查了整体思想和作图能力.

练习册系列答案
相关题目
 .
. 时,若函数
时,若函数 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围; ,
, ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 的值.
的值. .
. .
. ,,求△ABC的面积.
,,求△ABC的面积. ,且
,且 .(I)求
.(I)求 的值;(II)求函数
的值;(II)求函数 在[1,3]上的最小值和最大值.
在[1,3]上的最小值和最大值.