Question

【题目】【2017南通扬州泰州苏北四市高三二模】（本小题满分14分）

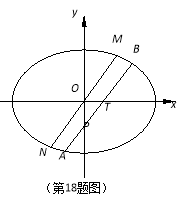
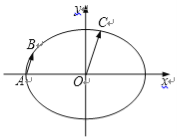
如图，在平面直角坐标系中，已知椭圆的离心率为，C为椭

圆上位于第一象限内的一点．

（1）若点的坐标为，求a，b的值；

（2）设A为椭圆的左顶点，B为椭圆上一点，且，求直线AB的斜率．

Answer 1

【答案】见解析

【解析】（1）因为椭圆的离心率为，

所以，即．①

又因为点在椭圆上，

所以． ② …… 3分

由①②解得．

因为，所以．……5分

（2）法一：由①知，，所以椭圆方程为，即．

设直线OC的方程为，，．

由得，

所以．因为，所以．……8分

因为，所以．可设直线的方程为．

由得，

所以或，得．……11分

因为，所以，于是，

即，所以．

所以直线AB的斜率为．……14分

法二：由（1）可知，椭圆方程为，则．

设，．

由，得，

所以，．……8分

因为点B，点C都在椭圆上，

所以

解得，，……12分

所以直线AB的斜率．……14分