题目内容
三、解答题(本大题共有3个小题,共40分。解答应写出文字说明、演算步骤或证明过程。)
13. (本小题满分13分)
已知命题
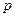 :方程
:方程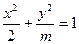 表示焦点在
表示焦点在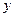 轴上的椭圆,命题
轴上的椭圆,命题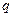 :关于x的方程
:关于x的方程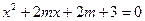 无实根,若“
无实根,若“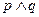 ”为假命题,“
”为假命题,“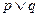 ”为真命题,求实数
”为真命题,求实数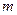 的取值范围.
的取值范围.
略

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
题目内容
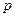 :方程
:方程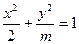 表示焦点在
表示焦点在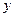 轴上的椭圆,命题
轴上的椭圆,命题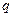 :关于x的方程
:关于x的方程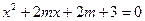 无实根,若“
无实根,若“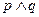 ”为假命题,“
”为假命题,“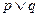 ”为真命题,求实数
”为真命题,求实数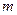 的取值范围.
的取值范围.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案