题目内容
A={x|x2+x-6=0},B={x|mx+1=0},且A∪B=A,则m的取值范围是分析:通过解二次方程化简集合A,利用A∪B=A?B⊆A;分类讨论求集合B中的一次方程,利用两个集合间的包含关系求出m的值.
解答:解:A={x|x2+x-6=0}={2,-3}
∵A∪B=A∴B⊆A
当m=0时,B=∅,满足B⊆A
当m≠0时,B={-
}
∵B⊆A
∴-
=2或-
=-3
解得m=-
或m=
故m的取值为{0,-
,
}
故答案为:{0,-
,
}
∵A∪B=A∴B⊆A
当m=0时,B=∅,满足B⊆A
当m≠0时,B={-
| 1 |
| m |
∵B⊆A
∴-
| 1 |
| m |
| 1 |
| m |
解得m=-
| 1 |
| 2 |
| 1 |
| 3 |
故m的取值为{0,-
| 1 |
| 2 |
| 1 |
| 3 |
故答案为:{0,-
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查解决集合间的关系时先化简各集合、考查A∪B=A?B⊆A、考查分类讨论的数学思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
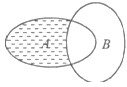 已知全集U=R,集合A={x|x2+x-2<0},B={x|0<x<3},则图中阴影部分所表示的集合为( )
已知全集U=R,集合A={x|x2+x-2<0},B={x|0<x<3},则图中阴影部分所表示的集合为( )| A、{x|-2<x≤0} | B、{x|0<x<1} | C、{x|1≤x<3} | D、{x|x≤-2或x≥3} |