题目内容
对于函数 (其中a为实数,x≠1),给出下列命题:
(其中a为实数,x≠1),给出下列命题:①当a=1时,f(x)在定义域上为单调增函数;
②f(x)的图象的对称中心为(1,a);
③对任意a∈R,f(x)都不是奇函数;
④当a=-1时,f(x)为偶函数;
⑤当a=2时,对于满足条件2<x1<x2的所有x1,x2总有f(x1)-f(x2)<3(x2-x1).
其中正确命题的序号为 .
【答案】分析:①由a=1,将函数用分离常数法转化,f(x)= ,其图象是由
,其图象是由 向右,向上平移一个单位得到的,再利用反比例函数的单调性得到结论.
向右,向上平移一个单位得到的,再利用反比例函数的单调性得到结论.
②用分离常数法转化, ,易得其图象关于(1,a)对称.
,易得其图象关于(1,a)对称.
③若为是奇函数,则图象关于原点对称,由②易知不正确.
④由a=-1,用分离常数法转化,f(x)= ,再用偶函数定义判断.
,再用偶函数定义判断.
⑤由a=2,用分离常数法转化,f(x)= ,易知在(1,+∞)上是减函数,再研究即得.
,易知在(1,+∞)上是减函数,再研究即得.
解答:解:①当a=1时,f(x)= ,是由
,是由 向右,向上平移一个单位得到的,不是单调函数,不正确.
向右,向上平移一个单位得到的,不是单调函数,不正确.
 ,其图象关于(1,a)对称,正确.
,其图象关于(1,a)对称,正确.
③由②知对称点的横坐标是1,不可能是0,所以不可能是奇函数,正确.
④当a=-1时,f(x)= ,定义域不关于原点对称,所以不可能为偶函数,不正确.
,定义域不关于原点对称,所以不可能为偶函数,不正确.
⑤当a=2时,f(x)= ,在(1,+∞)上是减函数,则在(2,+∞)上也是减函数
,在(1,+∞)上是减函数,则在(2,+∞)上也是减函数
∴对于满足条件2<x1<x2的所有x1,x2总有f(x1)-f(x2)<3(x2-x1).
故答案为:②③⑤
点评:本题主要考查形如: 的图象和性质,研究的方法是用分离常数法转化的为反比例型函数解决.
的图象和性质,研究的方法是用分离常数法转化的为反比例型函数解决.
 ,其图象是由
,其图象是由 向右,向上平移一个单位得到的,再利用反比例函数的单调性得到结论.
向右,向上平移一个单位得到的,再利用反比例函数的单调性得到结论.②用分离常数法转化,
 ,易得其图象关于(1,a)对称.
,易得其图象关于(1,a)对称.③若为是奇函数,则图象关于原点对称,由②易知不正确.
④由a=-1,用分离常数法转化,f(x)=
 ,再用偶函数定义判断.
,再用偶函数定义判断.⑤由a=2,用分离常数法转化,f(x)=
 ,易知在(1,+∞)上是减函数,再研究即得.
,易知在(1,+∞)上是减函数,再研究即得.解答:解:①当a=1时,f(x)=
 ,是由
,是由 向右,向上平移一个单位得到的,不是单调函数,不正确.
向右,向上平移一个单位得到的,不是单调函数,不正确. ,其图象关于(1,a)对称,正确.
,其图象关于(1,a)对称,正确.③由②知对称点的横坐标是1,不可能是0,所以不可能是奇函数,正确.
④当a=-1时,f(x)=
 ,定义域不关于原点对称,所以不可能为偶函数,不正确.
,定义域不关于原点对称,所以不可能为偶函数,不正确.⑤当a=2时,f(x)=
 ,在(1,+∞)上是减函数,则在(2,+∞)上也是减函数
,在(1,+∞)上是减函数,则在(2,+∞)上也是减函数∴对于满足条件2<x1<x2的所有x1,x2总有f(x1)-f(x2)<3(x2-x1).
故答案为:②③⑤
点评:本题主要考查形如:
 的图象和性质,研究的方法是用分离常数法转化的为反比例型函数解决.
的图象和性质,研究的方法是用分离常数法转化的为反比例型函数解决. 
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
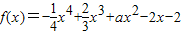 ,其中a为实常数,已知函数y=f(x)的图象在点(-1,f(-1))处的切线与y轴垂直.
,其中a为实常数,已知函数y=f(x)的图象在点(-1,f(-1))处的切线与y轴垂直.