题目内容
直线a与平面α所成的角为30°,直线b在平面α内,若直线a与b所成的角为θ,则( )
分析:根据题意,作出图形如图所示.由直线与平面所成角的定义,得到a与b所成角的最小值等于30°;由三垂线定理与两条直线垂直的判定,可得a与b所成角的最大值等于90°.由此得到本题的答案.
解答:解:设直线a在平面α的射影为直线c,在平面α内作直线d⊥c,由三垂线定理可得直线d⊥a.
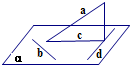
∵直线a与平面α所成的角为30°,
∴直线a与直线c所成的角为30°,等于平面α内的直线与直线a所成角的最小值.
直线b在平面α内,当b与直线d平行或重合时,可得a⊥b,直线a与b所成的角为90°,达到最大值;
当b与直线c平行或重合时,可得a、b所成的角为30°,达到最小值.
因此,直线a与b所成的角为φ的取值范围为30°≤θ≤90°.
故选:C

∵直线a与平面α所成的角为30°,
∴直线a与直线c所成的角为30°,等于平面α内的直线与直线a所成角的最小值.
直线b在平面α内,当b与直线d平行或重合时,可得a⊥b,直线a与b所成的角为90°,达到最大值;
当b与直线c平行或重合时,可得a、b所成的角为30°,达到最小值.
因此,直线a与b所成的角为φ的取值范围为30°≤θ≤90°.
故选:C
点评:本题给出直线与平面所成角的大小,求平面内的直线与已知直线所成角取值范围.着重考查了直线与平面所成角的定义、三垂线定理和异面直线所成角的定义等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1 的棱长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1 的棱长为1,线段B1D1上有两个动点E,F,且EF=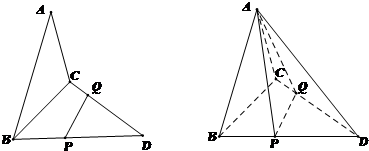 如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.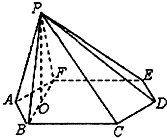 (2012•武清区一模)如图,六棱锥P-ABCDEF的底面ABCDEF是边长为l的正六边形,顶点P在底面上的射影是BF的中点O.
(2012•武清区一模)如图,六棱锥P-ABCDEF的底面ABCDEF是边长为l的正六边形,顶点P在底面上的射影是BF的中点O. 在P是直角梯形ABCD所在平面外一点,PA⊥平面ABCD,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PD与底面成30°角,BE⊥PD于E,求直线BE与平面PAD所成的角.
在P是直角梯形ABCD所在平面外一点,PA⊥平面ABCD,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PD与底面成30°角,BE⊥PD于E,求直线BE与平面PAD所成的角. ,
, 所成的角相等,那么平面
所成的角相等,那么平面 与
与 的位置关系是
的位置关系是 ∥
∥
 不一定平行于
不一定平行于
 不平行于
不平行于