题目内容
已知
=(x,1),
=(x-2,1),
=(2,m)
(1)若
∥
,
⊥
求实数x,m的值;
(2)当x∈[-1,1]时,
•
=
•
恒成立,试确定实数m的范围.
| a |
| b |
| c |
(1)若
| a |
| c |
| b |
| c |
(2)当x∈[-1,1]时,
| a |
| b |
| a |
| c |
(1)由
∥
得 mx-2=0
由
⊥
得 2(x-2)+m=0
解得 x=1,m=2
(2)∵
•
=x2-2x+1,
•
=2x+m
∴由题意得 x2-2x+1>2x+m在[-1,1]上恒成立.即m<x2-4x+1在[-1,1]上恒成立.
设g(x)=x2-4x+1,其图象的对称轴为直线x=2,
所以g(x)在[-1,1]上递减,g(x)min=g(1)=-2
故只需m<g(x)min,即m<-2.
| a |
| c |
由
| b |
| c |
解得 x=1,m=2
(2)∵
| a |
| b |
| a |
| c |
∴由题意得 x2-2x+1>2x+m在[-1,1]上恒成立.即m<x2-4x+1在[-1,1]上恒成立.
设g(x)=x2-4x+1,其图象的对称轴为直线x=2,
所以g(x)在[-1,1]上递减,g(x)min=g(1)=-2
故只需m<g(x)min,即m<-2.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
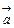 作最小的平移,使平移后的图象在[k
作最小的平移,使平移后的图象在[k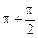 ,k
,k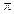 +
+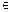 z)上递减,试求平移后的函数解析式和
z)上递减,试求平移后的函数解析式和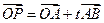 ,
,
 ,b=
,b= ,则向量
,则向量 ( )
( )  轴 B.平行于第一、三象限的角平分线
轴 B.平行于第一、三象限的角平分线 轴 D.平行于第二、四象限的角平分线
轴 D.平行于第二、四象限的角平分线  若
若 则实数
则实数 的值是
的值是  所成的比为1,则
所成的比为1,则 分向量
分向量 所成的比为
所成的比为
