题目内容
13．
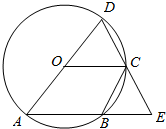如图，AD是⊙O的直径，B为⊙O上的一点，连接AB并延长至点E，使得AE=AD，连接DE，交⊙O于点C，连接OC．（1）求证：OC∥AE；
（2）若OC=AB，判断△BCE的形状并说明理由．
分析 （1）由已知得AC⊥DC，从而∠DAC=∠EAC=∠ACO，由此能证明OC∥AE．
（2）由OC=AB，OC∥AE，OA=OC，得四边形ABCO是菱形，∠A=60°，由此能证明△BCE是等边三角形．
解答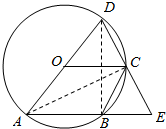 
（本小题满分8分）
（1）证明：∵AD是⊙O的直径，B为⊙O上的一点，连接AB并延长至点E，使得AE=AD，
连接DE，交⊙O于点C，连接OC，
∴AC⊥DC，∴∠DAC=∠EAC=∠ACO，
∴OC∥AE．…（4分）
（2）解：△BCE为等边三角形．
证明如下：
∵OC=AB，OC∥AE，∴四边形ABCO是平行四边形，
∵OA=OC，∴四边形ABCO是菱形，
∵AO=OD=OC，AD是直径，∴∠A=60°，∴△ADE是等边三角形，
∴∠E=60°，BC=BE，∴△BCE是等边三角形．…（8分）
点评 本题考查直线平行的证明，考查三角形形状的判断，是基础题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
1．将函数y=sin（2x-θ）的图象F向右平移$\frac{π}{3}$个单位长度得到图象F′，若F′的一条对称轴是直线x=$\frac{π}{4}$，则θ的一个可能取值是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{2}$ |
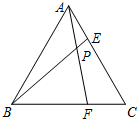等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连结AF，BE相交于点P．
如图所示的程序框图，运行相应的程序，若输入x的值为-4，则输出y的值为2．