题目内容
13.在△ABC中,已知cosA=$\frac{2\sqrt{5}}{5}$,C=$\frac{3π}{4}$,b=$\sqrt{2}$,若△ABC最大边的边长为$\sqrt{10}$,则△ABC的面积为1.分析 由已知利用同角三角函数基本关系式可求sinA,进而利用三角形内角和定理,两角和的正弦函数公式可求sinB,利用正弦定理可求c的值,进而利用三角形面积公式即可计算得解.
解答 解:在△ABC中,∵cosA=$\frac{2\sqrt{5}}{5}$,
∴可得:sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{5}}{5}$,
又∵C=$\frac{3π}{4}$,b=$\sqrt{2}$,
∴sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{\sqrt{5}}{5}×(-\frac{\sqrt{2}}{2})+$$\frac{2\sqrt{5}}{5}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{10}}{10}$,
∴由$\frac{b}{sinB}=\frac{c}{sinC}$,可得:c=$\frac{bsinC}{sinB}$=$\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{\frac{\sqrt{10}}{10}}$=$\sqrt{10}$,
S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×\sqrt{2}×\sqrt{10}×$$\frac{\sqrt{5}}{5}$=1.
故答案为:1.
点评 本题主要考查了同角三角函数基本关系式,三角形内角和定理,两角和的正弦函数公式,正弦定理,三角形面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
5.若直线ax+by-1=0与圆x2+y2=1相切,则点P(a,b)的位置是( )
| A. | 在圆上 | B. | 在圆外 | C. | 在圆内 | D. | 以上皆有可能 |
4.已知函数f(x)=aex-x2-(2a+1)x,若函数f(x)在区间(0,ln2)上有最值,则实数a的取值范围是( )
| A. | (-∞,-1) | B. | (-1,0) | C. | (-2,-1) | D. | (-∞,0)∪(0,1) |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为F(2,0),双曲线的渐近线y=±$\sqrt{3}$x,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{13}$=1 | B. | $\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
8.给出以下四个判断,其中正确的判断是( )
| A. | 函数f(x)的定义域关于原点对称是f(x)具有奇偶性的充分不必要条件 | |
| B. | 命题“若x≥4且y≥2,则x+y≥6”的逆否命题为“若x+y<6,则x<4且y<2” | |
| C. | 若p:?x≥0,x2-x+1>0,则¬p:?x<0,x2-x+1≤0 | |
| D. | 己知n∈N,则幂函数y=x3n-7为偶函数,且在x∈(0,+∞)上单调递减的充分必要条件为n=1 |
5.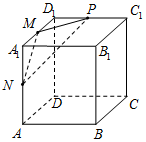 正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )
正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )
 正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )
正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $12\sqrt{3}$ |
2.已知集合A={x|log${\;}_{\frac{1}{2}}$(x+1)≥-2},B={x|$\frac{x+2}{1-x}$≥2},则 A∩B=( )
| A. | (-1,1) | B. | [0,1) | C. | [0,3] | D. | ∅ |