题目内容
11.设函数f(x)=-x2-3,g(x)=2xlnx-ax,且函数f(x)与g(x)在x=1处的切线平行.(Ⅰ)求函数g(x)在(1,g(1))处的切线方程;
(Ⅱ)当x>0时,g(x)-f(x)≥0恒成立,求实数a的取值.
分析 (Ⅰ)求出函数的导数,求出a的值,从而求出g(1),g′(1),求出切线方程即可;
(Ⅱ)问题转化为a≤2lnx+x+$\frac{3}{x}$恒成立,设h(x)=2lnx+x+$\frac{3}{x}$,(x>0),根据函数的单调性求出a的范围即可.
解答 解:(Ⅰ)f′(x)=-2x,g′(x)=2lnx+2-a,
∵函数f(x)与g(x)在x=1处的切线平行,
∴f′(1)=g′(1),解得:a=4,
故g(1)=-4,g′(1)=-2,
故函数g(x)在(1,g(1))处的切线方程是:2x+y+2=0;
(Ⅱ)x∈(0,+∞)时,由g(x)-f(x)≥0恒成立,
得x∈(0,+∞)时,2xlnx-ax+x3+3≥0,
即a≤2lnx+x+$\frac{3}{x}$恒成立,
设h(x)=2lnx+x+$\frac{3}{x}$,(x>0),
则h′(x)=$\frac{(x+3)(x-1)}{{x}^{2}}$,
x∈(0,1)时,h′(x)<0,h(x)递减,
x∈(1,+∞)时,h′(x)>0,h(x)递增,
故h(x)min=h(1)=4,
故a的范围是(-∞,4].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
相关题目
1.阅读如图程序框图,当输入x的值为2时,运行相应程序,则输出x的值为( )


| A. | 5 | B. | 11 | C. | 23 | D. | 47 |
2.如图所示,图中粗线画出的是某几何体的三视图,该几何体的体积是( )
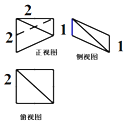

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
3.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点为F,过F作双曲线C渐近线的垂线,垂足为A,且交y轴于B,若$\overrightarrow{BA}=2\overrightarrow{AF}$,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
20.已知奇函数f(x)在[0,+∞)上是增函数,若f(lnx)<0,则( )
| A. | $\frac{1}{e}$<x<1或x>1 | B. | 1<x<e | C. | 0<x<e或x>e | D. | 0<x<1 |