题目内容
(12分)
如图,四棱锥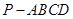 中,
中,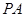 ⊥底面
⊥底面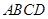 ,底面
,底面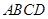 为梯形,
为梯形,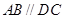 ,
,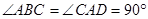 ,且
,且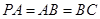 ,点
,点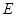 是棱
是棱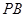 上的动点.
上的动点.
(Ⅰ)当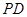 ∥平面
∥平面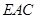 时,确定点
时,确定点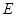 在
在 棱
棱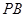 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角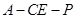 的余弦值.
的余弦值.
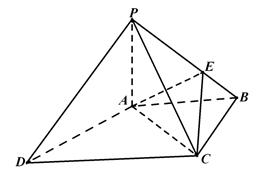
如图,四棱锥
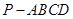 中,
中,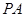 ⊥底面
⊥底面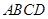 ,底面
,底面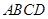 为梯形,
为梯形,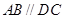 ,
,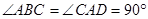 ,且
,且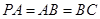 ,点
,点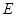 是棱
是棱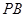 上的动点.
上的动点.(Ⅰ)当
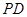 ∥平面
∥平面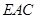 时,确定点
时,确定点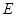 在
在 棱
棱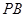 上的位置;
上的位置;(Ⅱ)在(Ⅰ)的条件下,求二面角
 的余弦值.
的余弦值.
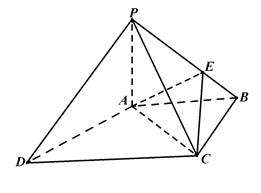
解:(Ⅰ)在梯形
 中,由
中,由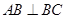 ,
,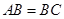 ,得
,得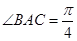 ,
,∴
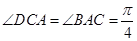 .又
.又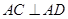 ,故
,故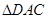 为等腰直角三角形.
为等腰直角三角形.∴
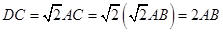 .
. 连接
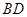 ,交
,交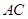 于点
于点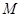 ,则
,则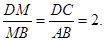
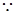
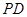 ∥平面
∥平面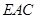 ,又平面
,又平面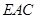
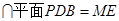 ,∴
,∴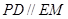 .
.在
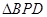 中,
中,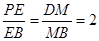 ,
,即
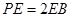 时,
时,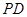 ∥平面
∥平面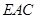 . 6分
. 6分(Ⅱ)方法一:在等腰直角
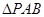 中,取
中,取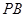 中点
中点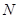 ,连结
,连结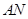 ,则
,则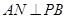 .∵平面
.∵平面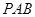 ⊥平面
⊥平面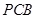 ,且平面
,且平面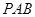
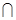 平面
平面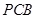 =
=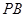 ,∴
,∴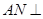 平面
平面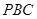 .
.在平面
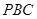 内,过
内,过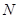 作
作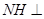 直线
直线 于
于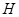 ,连结
,连结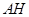 ,由
,由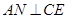 、
、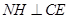 ,得
,得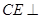 平面
平面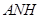 ,故
,故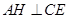 .∴
.∴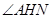 就是二面角
就是二面角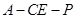 的平面角.
的平面角. 在
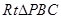 中,设
中,设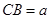 ,则
,则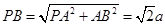 ,
,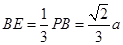 ,
,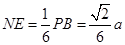 ,
, ,
,由
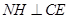 ,
,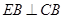 可知:
可知: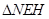 ∽
∽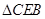 ,∴
,∴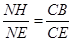 ,
,代入解得:
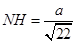 .
.
在
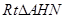 中,
中,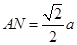 ,∴
,∴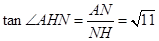 ,
,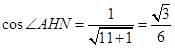 .
.∴二面角
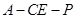
 的余弦值为
的余弦值为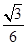 .
. 
 12分
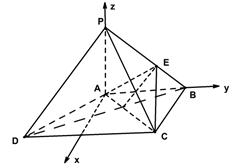
12分方法二:以
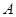 为原点,
为原点,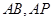 所在直线分别为
所在直线分别为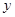 轴、
轴、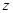 轴,
轴, 如图建立空间直角坐标系.
如图建立空间直角坐标系.设
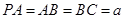 ,则
,则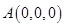 ,
,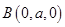 ,
,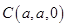 ,
,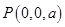 ,
,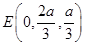 .
.设
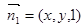 为平面
为平面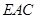 的一个法向量,则
的一个法向量,则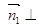
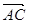 ,
,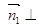
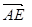 ,∴
,∴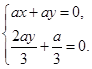 ,解得
,解得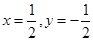 ,∴
,∴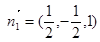 .
. 设
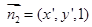 为平面
为平面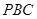 的一个法向量,则
的一个法向量,则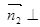
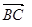 ,
,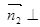
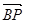 ,
,又
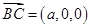 ,
,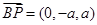 ,∴
,∴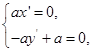 ,解得
,解得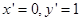
∴
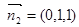 .
.
∴二面角
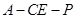 的余弦值为
的余弦值为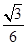 . 12分
. 12分略

练习册系列答案
相关题目
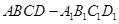 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高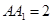 .求:
.求: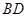 与
与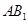 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示); 的体积.
的体积.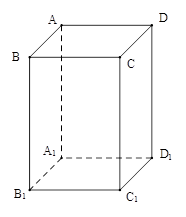
 的底面为直角梯形,
的底面为直角梯形, ,
,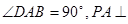 底面
底面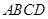 ,且
,且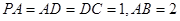 ,
,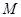 是
是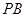 的中点.
的中点.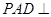 面
面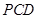 ;
;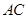 与
与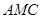 与面
与面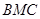 所成二面角的余弦值.
所成二面角的余弦值.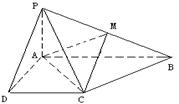
 ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、
ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、 BC的中点,M为棱AA1上的点。
BC的中点,M为棱AA1上的点。 的大小。
的大小。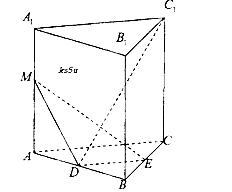
 β
β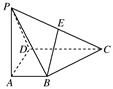
 ,
, ⊥
⊥ ,
, ⊥
⊥ ⊥
⊥ ;
; 所成的角相等;
所成的角相等; 在
在 .
.
 不共面的射线
不共面的射线 两两之间的夹角都是
两两之间的夹角都是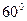 ,则平面
,则平面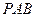 与平面
与平面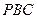 所成的
所成的