题目内容
 (2012•包头一模)如图椭圆C:
(2012•包头一模)如图椭圆C:| x2 |
| 4 |
| y2 |
| 3 |
(Ⅰ)证明:直线DE与直线BM的交点在椭圆C上;
(Ⅱ)若过点E的直线交椭圆于R,S两点,K为R关于x轴的对称点(R,K,E不共线),问:直线KS是否经过x轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
分析:(Ⅰ)求出直线DE、BM的方程,从而可得交点坐标,代入椭圆方程验证即可;
(Ⅱ)确定直线SK的方程,求得y=0时,横坐标为定值,即可得到结论.
(Ⅱ)确定直线SK的方程,求得y=0时,横坐标为定值,即可得到结论.
解答:(Ⅰ)证明:由题意,得A(2,0),B(0,
),D(0,-
),E(1,0),M(2,
),
所以直线DE的方程y=
x-
,直线BM的方程为y=-
x+
,------(2分)
由
,得
,
所以直线DE与直线BM的交点坐标为(
,
),---------------(4分)
因为
+
=1,所以点(
,
)在椭圆C:
+
=1上.---------(6分)
(Ⅱ)设RS的方程为y=k(x-1),代入C:
+
=1,得(3+4k2)x2-8k2x+4k2-12=0,
设R(x1,y1),S(x2,y2),则K(x1,-y1),x1+x2=
,x1x2=
,
直线SK的方程为y-y2=
(x-x2),令y=0,得x=
,
将y1=k(x1-1),y2=k(x2-1)代入上式得x=
=4,
所以直线SK经过x轴上的点(4,0).---------(12分)
| 3 |
| 3 |
| ||
| 2 |
所以直线DE的方程y=
| 3 |
| 3 |
| ||
| 4 |
| 3 |
由
|
|
所以直线DE与直线BM的交点坐标为(
| 8 |
| 5 |
3
| ||
| 5 |
因为
(
| ||
| 4 |
(
| ||||
| 3 |
| 8 |
| 5 |
3
| ||
| 5 |
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设RS的方程为y=k(x-1),代入C:
| x2 |
| 4 |
| y2 |
| 3 |
设R(x1,y1),S(x2,y2),则K(x1,-y1),x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
直线SK的方程为y-y2=
| y2+y1 |
| x2-x1 |
| y1x2+y2x1 |
| y2+y1 |
将y1=k(x1-1),y2=k(x2-1)代入上式得x=
| 2x1x2-(x1+x2) |
| x1+x2-2 |
所以直线SK经过x轴上的点(4,0).---------(12分)
点评:本题考查直线方程,考查点与椭圆的位置关系,考查直线恒过定点,确定直线的方程是关键.

练习册系列答案
相关题目
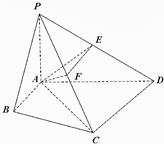 (2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
(2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1. (2012•包头一模)函数f(x)=sin(ωx+?)(其中
(2012•包头一模)函数f(x)=sin(ωx+?)(其中