题目内容
2.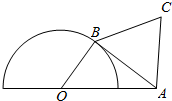 如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.
如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.(1)若∠AOB=θ(单位:rad),分别求出三角形ABC和三角形OAB的面积;
(2)求三角形ABC和三角形OAB的面积之比的最小值.
分析 (1)利用余弦定理,求出AB的长,代入等边三角形面积公式,可得三角形ABC的面积,根据三角形OAB的面积为:$\frac{1}{2}OA•OB•sin∠AOB$可得三角形OAB的面积;
(2)由(1)得到三角形ABC和三角形OAB的面积之比,根据三角函数的图象和性质,可得其最小值.
解答 解:(1)∵半圆O的直径为2,OA=2,∠AOB=θ,
∴OB=1,
AB=$\sqrt{{OA}^{2}+{OB}^{2}-2OA•OB•cos∠AOB}$=$\sqrt{5-cosθ}$,
则三角形ABC的面积为:$\frac{\sqrt{3}}{4}(5-cosθ)$
故三角形OAB的面积为:$\frac{1}{2}OA•OB•sin∠AOB$=sinθ;
(2)由(1)得:三角形ABC和三角形OAB的面积之比k=$\frac{\frac{\sqrt{3}}{4}(5-cosθ)}{sinθ}$,
则k′=$\frac{\frac{\sqrt{3}}{4}(1-5cosθ)}{si{n}^{2}θ}$,
故当cosθ=$\frac{1}{5}$,sinθ=$\frac{2\sqrt{6}}{5}$时,
k取最小值$\frac{3}{2}\sqrt{2}$
点评 本题考查的知识点是三角形的面积公式,三角函数的最小值,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列函数既是奇函数又是(0,1)上的增函数的是( )
| A. | y=-x | B. | y=x2 | C. | y=sinx | D. | y=cosx |
13.函数f(x)=$\frac{sinx}{sinx+cosx}$在区间[0,$\frac{π}{2}$]上的最大值与最小值分别是 ( )
| A. | 1,0 | B. | $\frac{1}{2}$,0 | C. | 0,-1 | D. | 1,$\frac{1}{2}$ |
16.下列函数f(x)中,满足“?x1x2∈(0,+∞)且x1≠x2有(x1-x2)[f(x1)-f(x2)]<0”的是( )
| A. | f(x)=$\frac{1}{x}$-x | B. | f(x)=x3 | C. | f(x)=lnx+ex | D. | f(x)=-x2+2x |