题目内容
某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉的价格为3200元,面粉的保管等其它费用为平均每吨每天3元,购买面粉每次需要 支付运费900元。
支付运费900元。
(Ⅰ)求该厂每隔多少天购买一次面粉,才能使平均每天支付的总费用 最少?最少费用为多少?
最少?最少费用为多少?
(Ⅱ)某提供面粉的公司规定:当一次购买面粉不少于120吨时,价格可享受9.5折优惠,问该厂是否考虑利用此优惠条件?请说明理由。
解:(Ⅰ)设该厂每 隔
隔 天
天 购买一次面粉,其购买量为
购买一次面粉,其购买量为 吨,由题意知,面粉的保管等其它费用为
吨,由题意知,面粉的保管等其它费用为 ……
…… ……2分
……2分
设平均每天所支付的总费用为 元,则
元,则
 ……5分
……5分
当且仅当
该厂每隔10天购买一次面粉,才能使平均每天所支付的总费用最少为19389元。 ……6分
……6分
(Ⅱ)若厂家利用此优惠条件,则至少每隔20天购买一次面粉,设该厂利用优惠条件后,每隔 天购买一次面粉,平均每天所支付的总费用为
天购买一次面粉,平均每天所支付的总费用为 元,则
元,则 

令 ,则
,则 为增函数,
为增函数, 18474<19389.
18474<19389.
所以该厂可考虑利用此优惠条件。 ……12分
解析

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
不等式组 ,所表示的平面区域的面积等于( )
,所表示的平面区域的面积等于( )
A. | B. | C. | D. |
在平面直角坐标系中,不等式 表示的平面区域的面积是
表示的平面区域的面积是
| A.8 | B.4 | C. | D. |
已知点P(x,y)在不等式组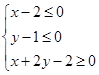 表示的平面区域上运动,则x-y的取值范围是( ).
表示的平面区域上运动,则x-y的取值范围是( ).
| A.[-2,-1] | B.[-2,1] | C.[-1,2] | D.[1,2] |
设变量 ,
, 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值为
的最小值为
| A.2 | B.3 | C.4 | D.5 |
 ,
, ,求证:
,求证: ;
; ,
, ,求证:
,求证: .
.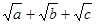 的最大值.
的最大值. ,求证:
,求证:
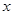 万件与投入技术改革费用
万件与投入技术改革费用 万元(
万元( )满足
)满足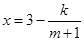 (
(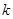 为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的
为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的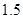 倍(生产成本包括固定投入和再投入两部分资金).
倍(生产成本包括固定投入和再投入两部分资金). 万元表示为技术改革费用
万元表示为技术改革费用