题目内容
在平面直角坐标系中,不等式 表示的平面区域的面积是
表示的平面区域的面积是
| A.8 | B.4 | C. | D. |
A
解析试题分析:由|y-2|+|x+2|≤2得|y-2|≤2-|x+2|,
若y≥2,则不等式等价为y-2≤2-|x+2|,即y≤4-|x+2|,
若y<2,则不等式等价为-(y-2)≤2-|x+2|,即y≥|x+2|,
作出不等式组对应的平面区域如图:
则对应的区域为正方形,其中C(-2,0),D(0,2),
|CD|= ,
,
则正方形的面积 ;故选:A.
;故选:A.
考点:简单线性规划.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设x、y满足约束条件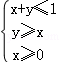 ,则z=2x﹣y的最大值为( ).
,则z=2x﹣y的最大值为( ).
| A.0 | B.2 | C.3 | D. |
已知x,y满足条件 (k为常数),若目标函数
(k为常数),若目标函数 的最大值为8,则k=
的最大值为8,则k=
A. | B. | C. | D.6 |
若实数x, 满足不等式组
满足不等式组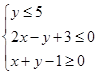 ,则z=|x|+2
,则z=|x|+2 的最大值是( )
的最大值是( )
| A.10 | B.11 | C.13 | D.14 |
若不等式组 ,表示的平面区域是一个三角形区域,则
,表示的平面区域是一个三角形区域,则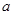 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. 或 或 |
已知变量x,y满足的不等式组 表示的是一个直角三角形围成的平面区域,则实数k=( )
表示的是一个直角三角形围成的平面区域,则实数k=( )
A.- | B. | C.0 | D.- 或0 或0 |
 支付运费900元。
支付运费900元。 +
+ 的最大值;
的最大值; +
+ 最大值为2
最大值为2 ,求正数a的值.
,求正数a的值.