题目内容
已知数列{an}满足,anan+1=n(n-1)(an+1-an),且a1=0,a2=1.
(1)求证:数列{an}是等差数列;
(2)设bn=2 an-34,求数列{|bn|}的前n项和Sn.
(1)求证:数列{an}是等差数列;
(2)设bn=2 an-34,求数列{|bn|}的前n项和Sn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)a1=0,a2=1,依题意只需证明?n∈N*,只需证an2+an-n(n-1)=0,即只需证an=n-1或an=-n,由此利用分析法能证明数列{an}是等差数列.
(2)由an=n-1,知bn=2n-1-34,由此能求出数列{|bn|}的前n项和Sn.
(2)由an=n-1,知bn=2n-1-34,由此能求出数列{|bn|}的前n项和Sn.
解答:
(1)证明:∵a1=0,a2=1,依题意只需证明?n∈N*,
an+1-an=a2-a1=1,…(1分)
∵anan+1=n(n-1)(an+1-an),
∴an+1=
,n>1,
∴只需证an+1-an=
=1,n>1.…(3分)
即只需证an2=n(n-1)-an,即只需证an2+an-n(n-1)=0,
即只需证an=n-1或an=-n,…(5分)
∵an=-n不符合a2=1,∴只需证an=n-1.
数列{n-1}是等差数列,且满足a1=0,a2=1,以上各步都可逆
∴数列{an}是等差数列 …(7分)
(2)解:由(1)可知an=n-1,∴bn=2n-1-34,…(8分)
设数列{bn}的前n项和为Tn,
数列{2n-1}是首项为1,公比为2的等比数列,数列{34}是常数列
∴Tn=b1+b2+…+bn=
-34n=2n-34n-1,…(9分)
令bn=2n-1-34>0,∴n>6,∵数列{bn}是递增数列
∴数列{bn}前6项为负,以后各项为正 …(10分)
∴当n≤6时,Sn=-Tn=-2n+34n+1,…(11分)
当n>6时,Sn=Tn-2T6=2n-34n-283.…(12分)
∴Sn=
.…(13分)
an+1-an=a2-a1=1,…(1分)
∵anan+1=n(n-1)(an+1-an),
∴an+1=
| n(n-1)an |
| n(n-1)-an |
∴只需证an+1-an=
| an2 |
| n(n-1)-an |
即只需证an2=n(n-1)-an,即只需证an2+an-n(n-1)=0,
即只需证an=n-1或an=-n,…(5分)
∵an=-n不符合a2=1,∴只需证an=n-1.
数列{n-1}是等差数列,且满足a1=0,a2=1,以上各步都可逆
∴数列{an}是等差数列 …(7分)
(2)解:由(1)可知an=n-1,∴bn=2n-1-34,…(8分)
设数列{bn}的前n项和为Tn,
数列{2n-1}是首项为1,公比为2的等比数列,数列{34}是常数列
∴Tn=b1+b2+…+bn=
| 1-2n |
| 1-2 |
令bn=2n-1-34>0,∴n>6,∵数列{bn}是递增数列
∴数列{bn}前6项为负,以后各项为正 …(10分)
∴当n≤6时,Sn=-Tn=-2n+34n+1,…(11分)
当n>6时,Sn=Tn-2T6=2n-34n-283.…(12分)
∴Sn=
|
点评:本题考查等差数列的证明,考查数列的前n项和的求法,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
执行如图程序框图,则输出的n值为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b∈R,下列四个条件中,使a<b成立的必要而不充分的条件是( )
| A、|a|<|b| |
| B、2a<2b |
| C、a<b-1 |
| D、a<b+1 |
若P的Q的北偏东44°50′,则Q在P的( )
| A、东偏北45°10′ |
| B、东偏北45°50′ |
| C、南偏西44°50′ |
| D、西偏南45°50′ |
下列式子正确的是( )
A、a2+
| ||||||
B、sinx+
| ||||||
C、
| ||||||
D、x+
|
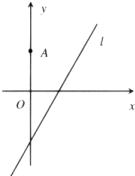 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上. 阅读如图所示算法:
阅读如图所示算法: