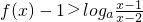题目内容
设f(x)=logax(a>0,a≠1),若f(x1)+f(x2)+…+f(xn)=1,(xi∈R,i=1,2,…,n),则f(x12)+f(x22)+…+f(xn2)的值等于
- A.

- B.1
- C.2
- D.2loga2
C
分析:由题意f(x1)+f(x2)+…f(xn)=1,f(x)=logax,根据对数的运算性质可得,x1x2…xn=a,而f(x12)+f(x22)+…+f(xn2)=logax12+…+logaxn2=loga(x12•x22…xn2)=2loga(x1x2…xn),从而可求.
解答:∵f(x1)+f(x2)+…f(xn)=1,f(x)=logax
∴loga(x1•x2…xn)=1
∴x1x2…xn=a
∴f(x12)+f(x22)+…+f(xn2)=logax12+…+logaxn2
=loga(x12•x22…xn2)=2loga(x1x2…xn)=2
故选C.
点评:本题主要考查了对数的运算性质,解题的关键是熟练掌握并能灵活利用对数的运算性质,由已知先求出x1x2…xn=a,再根据对数的运算性质代入,f(x12)+f(x22)+…+f(xn2)=logax12+…+logaxn2
=loga(x12•x22…xn2)=2loga(x1x2…xn)可求.
分析:由题意f(x1)+f(x2)+…f(xn)=1,f(x)=logax,根据对数的运算性质可得,x1x2…xn=a,而f(x12)+f(x22)+…+f(xn2)=logax12+…+logaxn2=loga(x12•x22…xn2)=2loga(x1x2…xn),从而可求.
解答:∵f(x1)+f(x2)+…f(xn)=1,f(x)=logax
∴loga(x1•x2…xn)=1
∴x1x2…xn=a
∴f(x12)+f(x22)+…+f(xn2)=logax12+…+logaxn2
=loga(x12•x22…xn2)=2loga(x1x2…xn)=2
故选C.
点评:本题主要考查了对数的运算性质,解题的关键是熟练掌握并能灵活利用对数的运算性质,由已知先求出x1x2…xn=a,再根据对数的运算性质代入,f(x12)+f(x22)+…+f(xn2)=logax12+…+logaxn2
=loga(x12•x22…xn2)=2loga(x1x2…xn)可求.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目