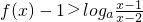Question

设f（x）=log_a（1+x）+log_a（3-x）（a＞0，a≠1），且f（1）=2．
（1）求a的值及f（x）的定义域．
（2）求f（x）在区间[0，

3

2

]上的值域．

Answer 1

分析：（1）由f（1）=2求得a的值，由对数的真数大于0求得f（x）的定义域；
（2）判定f（x）在（-1，3）上的增减性，求出f（x）在[0，

3

2

]上的最值，即得值域．

解答：解：（1）∵f（x）=log_a（1+x）+log_a（3-x），
∴f（1）=log_a2+log_a2=log_a4=2，∴a=2；
又∵

1+x＞0 3-x＞0

，∴x∈（-1，3），
∴f（x）的定义域为（-1，3）．
（2）∵f（x）=log₂（1+x）+log₂（3-x）=log₂[（1+x）（3-x）]=log₂[-（x-1）²+4]，
∴当x∈（-1，1]时，f（x）是增函数；
当x∈（1，3）时，f（x）是减函数，
∴f（x）在[0，

3

2

]上的最大值是f（1）=log₂4=2；
又∵f（0）=log₂3，f（

3

2

）=log₂

15

4

=-2+log₂15，
∴f（0）＜f（

3

2

）；
∴f（x）在[0，

3

2

]上的最小值是f（0）=log₂3；
∴f（x）在区间[0，

3

2

]上的值域是[log₂3，2]．

点评：本题考查了求函数的定义域和值域的问题，利用对数函数的真数大于0可求得定义域，利用函数的单调性可求得值域．